Gaussian formula

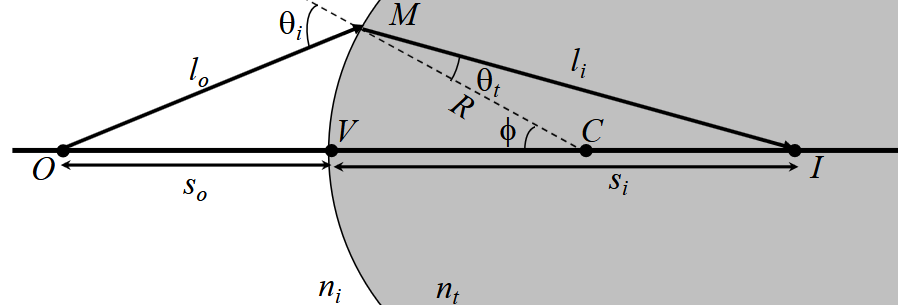
In geometric optics, the Gaussian formula provides a relationship between the distance of an object and the distance of an image, given an optical interface between two media: Important note: the positioning of the image point $s_i$ is entirely dependent on whether it’s a real or virtual image. If it’s a real image, we position it opposite to the object. If it’s a virtual image, we position it on the same side as the object.

The formula for a spherical interface is given by the following. In practice, we use the second.

$$\frac{s_o}{n_i(s_o+R)}=\frac{s_i}{n_t(s_i-R)}$$ $$\frac{n_i}{s_o}+\frac{n_t}{s_i}=\frac{n_t-n_i}{R}$$

This only holds if the paraxial approximation (or small angle approximation) holds, which is when we approximate with the first-order Taylor series expansion:

$$\sin \theta \approx \theta$$ $$\cos \theta \approx 1$$

It holds when:

• Rays stay roughly close to and nearly parallel with the optical axis (usually angles <15 degrees).
• Thin lenses or mirrors with relatively large focal lengths compared to their diameter.