When we think about sorting algorithms, we think about algorithms that put elements of a list (either an array or linked list) into some order (usually numerically or lexicographically).
A stable sorting algorithm preserves the relative order of elements. The correctness of most sorting algorithms can be proved with strong induction.
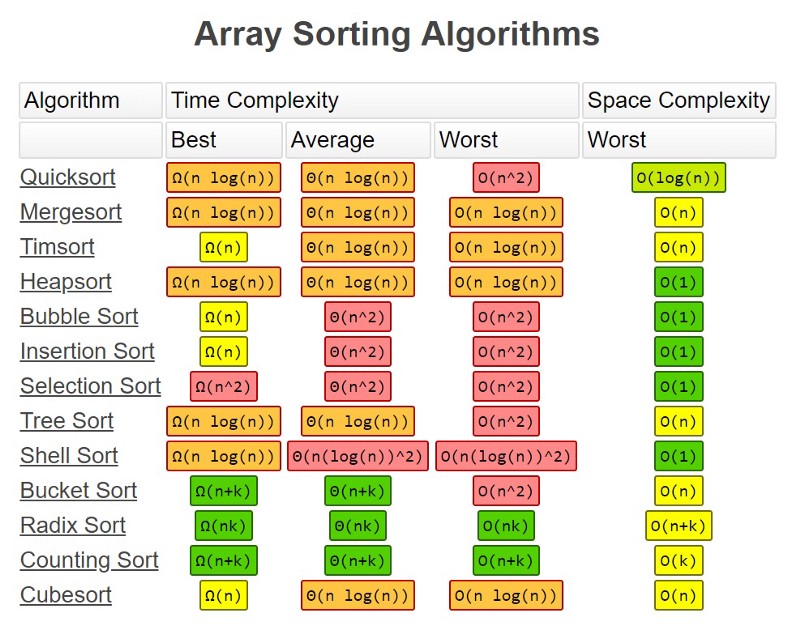
In terms of time complexity, consider the chart below. The primary implications of this:
- If our problem is known to restrict values to integers, we can use linear time sorting algorithms like radix sort or counting sort. We prefer radix sort over counting sort if the values of the array are sparse (i.e., on a number line they aren’t close together).
- Otherwise, we should pick an algorithm. Formally, we shouldn’t pick quicksort, because its worst case time complexity is . Choose something like mergesort or heapsort!
List
Comparison-based sorting
Many sorting algorithms are comparison-based, where we’re only permitted to use and equality operations. By theorem, any comparison-based algorithm requires comparisons in the worst-case.
We can model these algorithms as a decision tree. If there are elements in each list, then there are leaves in the decision tree (which corresponds to each possible permutation of the list).
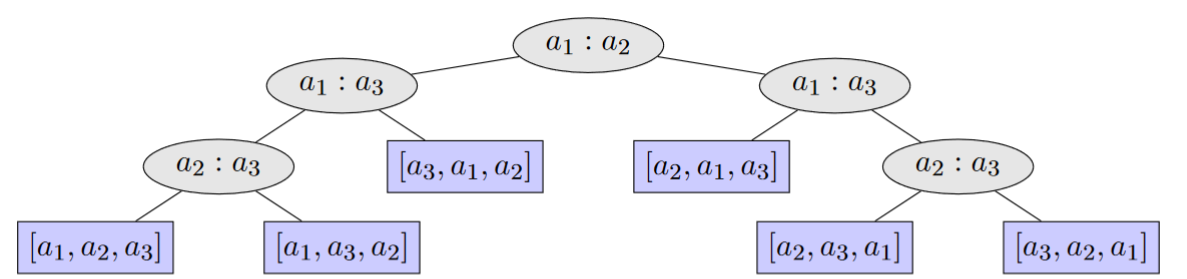In the worst case, we need to traverse the height of the decision tree. We can then prove that .
Language-specific
In C++, the standard library (in <algorithm>) provides an sorting algorithm with std::sort(). We can pass in either two iterators, or the structure itself. Note that pairs, tuples, are primarily sorted by the first element, then by successive elements. For user-defined structs, we need to overload with an operator> function, custom function, or lambda.
Mainly, the best way is to use a comparison function.
operator>is less preferred for modern C++.
std::stable_sort() takes the same parameters, but sorts while preserving the relative order of the elements.