Insertion sort

Insertion sort is a primitive sorting algorithm that sorts in ascending order. The idea is that we do $n$ passes for each element, then another $n$ iterations to check if its sorted.

It has an time complexity of $O(n^2)$ in the average-case and $O(n)$ in the worst-case. It’s slow in the worst case! So we use other algorithms.

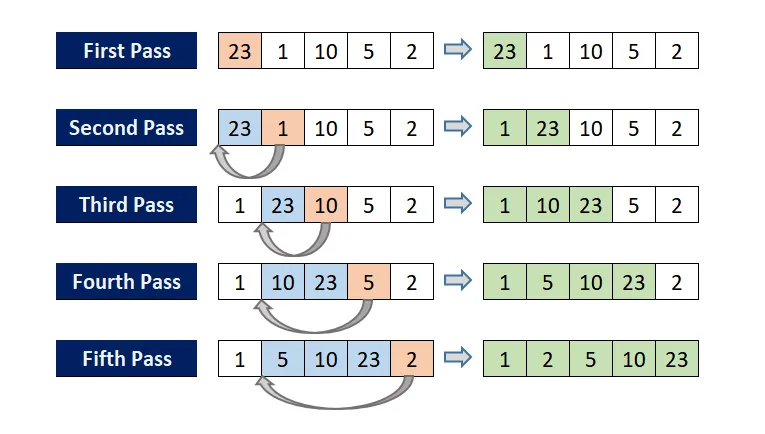
Implementation

Below is an implementation in C++:

void insertionSort (std::vector<int> list) {
	for (int top = 1; top < list.size(); top++) {
		int key = list[top];
		int index_of_empty_slot = top;
		while (index_of_empty_slot > 0 
				and key < list[index_of_empty_slot - 1]) {
			// shift data to the right to make space
			list[index_of_empty_slot] = list[index_of_empty_slot - 1];
			index_of_empty_slot--;
		}
		list[index_of_empty_slot] = key;
	}
}

Proof

For correctness, we can use a loop invariant that suggests: at the start of each iteration of the for loop, the sub-array list[0:i - 2] consists of the elements originally in that sub-array but in sorted order.¹

• Base case: we have top = 1. Since we’re dealing with a single element-large sub-array, this is obviously already sorted.
• In the loop: intuitively this holds by how it works. We slowly move the values one by one until it finds a proper position for list[i].
• Termination: the loop terminates after we exceed list.size(). This tells us that the subarray list[0:n - 1] contains the same elements but sorted in the loop.

Footnotes

1. From CLRS’ Introduction to Algorithms. ↩