Interference

In wave optics, interference is defined as the superposition of two or more coherent light waves that result in a spatial intensity modulation. It is formed by the wave superposition of two electric fields: ${\vec{E}}_{\text{total}}={\vec{E}}_1+{\vec{E}}_2$.

${\vec{E}}_1^{\ast }$ == complex conjugate

• Optical path difference: phase difference between beams depends on their path difference

Basics

For the time average of the interference term to be non-zero,¹ we must meet all of the following conditions.

• ${\vec{E}}_1,{\vec{E}}_2$ are non-orthogonal. They have non-orthogonal polarisations and ideally the same polarisations.
• $|{\omega }_2-{\omega }_1|$ should be sufficiently small, i.e., small enough for the detector to ignore. Otherwise, the $\cos$ term will change too fast and the detector cannot follow it. Ideally ${\omega }_1={\omega }_2$.
  • i.e., $\Delta \omega /2\pi$ should be less than the bandwidth of the detector.
• And ${\phi }_2-{\phi }_1$ should be sufficiently stable (very slow-varying). Ideally ${\phi }_2-{\phi }_1$ is constant. This is called the coherence condition.
  • In general, this is basically impossible to satisfy with two independent light sources. Thus, all practical interferometer set-ups use beams from the same source to satisfy this condition.

If we assume all of the conditions hold, then:

$$I_{\text{total}}=I_1+I_2+2\sqrt{I_1{I}_2}\cos \delta$$

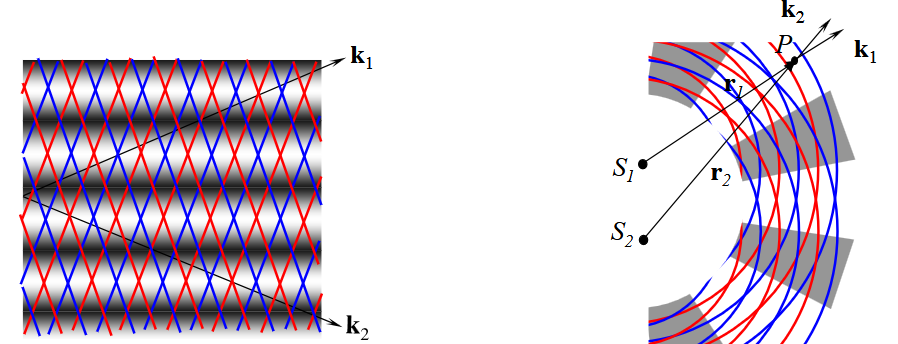
where $\delta$ is a phase difference (see OPL). For plane waves and circular waves, respectively:

$$\delta =({\vec{k}}_2-{\vec{k}}_1)\cdot \vec{r}+({\phi }_2-{\phi }_1)$$ $$\delta =(k_2-k_1)r+({\phi }_2-{\phi }_1)$$

We call the $kr$ term the difference in optical path length and the $\phi$ as the source phase difference.

This $\delta$ determines the maximum or minimum of the intensity that essentially produces a sinusoid between the max and min of the intensity.

• When $\delta =2m\pi$, we have the maximum intensity. This causes a bright fringe (or constructive interference).
• When $\delta =2m\pi +\pi$, then we have the minimum intensity. This causes a dark fringe (or destructive interference).
• For the special case of if $I_1=I_2=I_o$, then I_\max = 4I_o and I_\min = 0.

The term $m$ is called the order of the fringe. For circular fringes, $m$ is higher for fringes closer to the centre, than for fringes at the edges.

Computations

One of the key parameters we want to compute are the fringe distances. We can do this with two wavefunctions. We want to find $\delta$ from the wavefunctions, then see what $\delta$ is a function of. We can take the bright fringe condition, where $\delta =2m\pi$, then solve for the parameter that $\delta$ is a function of.

Footnotes

1. We use the time average and not the term itself because light oscillates with an incredibly high frequency, so we can’t observe the exact value anyways. ↩