Coherence

A coherent light source produces waves that maintain a constant phase relationship (spatially and temporally) over a period of time and across the wavefront. A common type of coherent light source is a laser.

• Temporal coherence describes how monochromatic the light is (i.e., how precise its single wavelength is). In practice, sources have a narrow but finite spectral width.
• Spatial coherence describes the correlation between waves at different points across the wavefront. High spatial coherence means the phase difference between any two points on the wavefront remains constant over time.

The coherence condition for the interference of light is when the phase difference between two beams ${\phi }_2-{\phi }_1$ is stable, i.e., it is not time varying. This is a necessary, but not sufficient (i.e., there must be other conditions), condition for interference. We say that if ${\phi }_2-{\phi }_1$ is fixed, then the two waves are mutually coherent. If it changes randomly, then the two waves (or two sources) are mutually incoherent.

We say that monochromatic waves (with a single frequency) of the same frequency must always be mutually coherent, since its phase at any time/location is completely predictable. However, coherence is generally not satisfied with real light sources, since practical light sources are not monochromatic (not temporally coherence) and are not point sources (not spatially coherent). Practical light sources are instead quasi-monochromatic, i.e., they have a mostly close frequency spectrum, but not the Dirac delta of an ideal source. 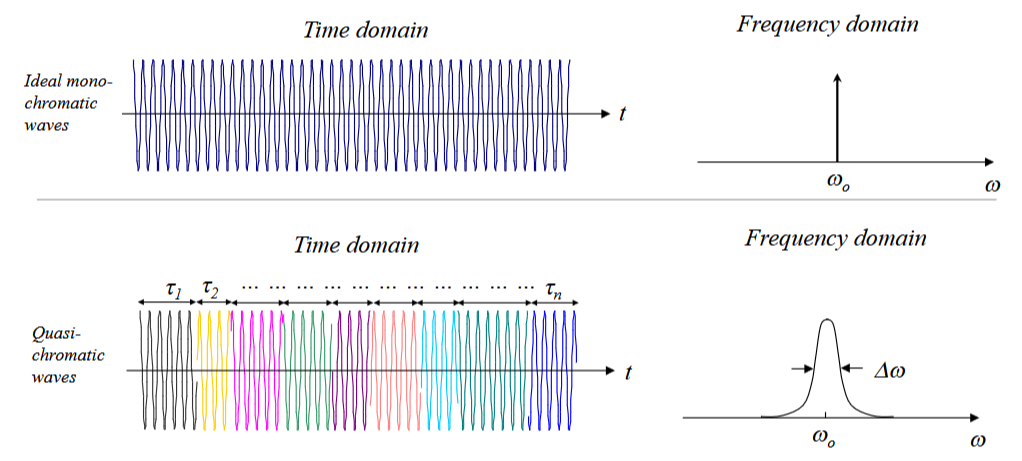This is essentially made up of single-frequency “trains” of short durations, where ${\tau }_i$ is a random variable. We define the bandwidth of the wave as $\Delta \omega$, and ${\tau }_c$ as the average duration of the wave trains. Then:

$${\tau }_c\sim \frac{2\pi }{\Delta \omega }$$

We call ${\tau }_c$ the coherence time. In interferometer set-ups (like the Michelson interferometer), we do amplitude splitting of a single quasi-monochromatic wave. But to interfere, the OPL difference must be such that the time delay between the two waves is less than ${\tau }_c$. Then, the temporal coherence length (or longitudinal coherence length) is:

$$l_c=c{\tau }_c$$

For coherence, we need $\Delta \text{OPL}<l_c$.

The spatial c