Thevenin's theorem

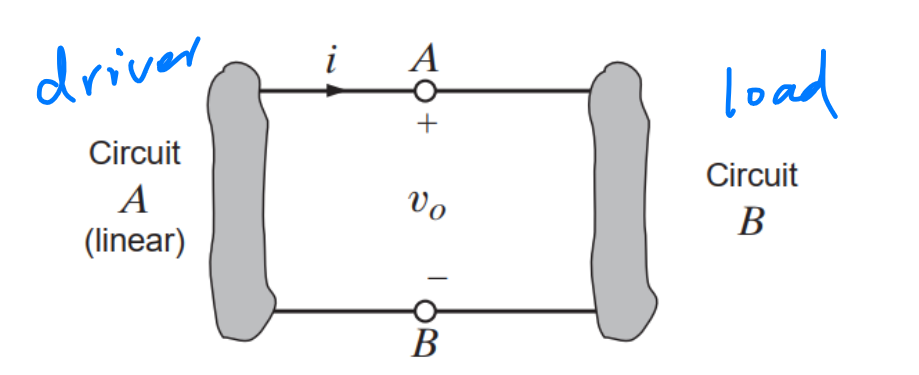
Thevenin’s theorem tells us that any linear circuit at terminals $A-B$ is equivalent to a circuit with a voltage source $V_{th}$ in series with a resistor $R_{th}$. An analogous theorem is Norton’s theorem, with a current source instead. 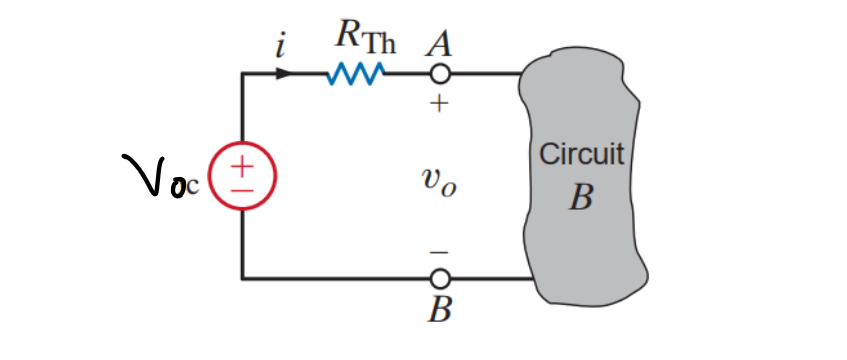A handy set of equations are:

$$v_o=v_{oc}-R_{th}i$$ $$R_{th}=\frac{V_{oc}}{I_{sc}}$$

Observe that the i-v characteristic for both Thevenin and Norton circuits follows:

$$i=\frac{v_{out}}{R_{th}}-\frac{v}{R_{Th}}$$

So $R_{Th}$ is as given, and $v_{Th}=\frac{v_{out}}{R_{Th}}{R}_N$.

Process

For circuits with only independent sources:

1. Remove load, then find $v_{oc}$ using simplifications and source transformation.
2. Then, to find $R_{th}$, we set all independent sources to zero and find the equivalent resistance.

For circuits with only dependent sources:

1. Assume some 1 V or 1 A source at the terminal and determine the dependent output. The choice of current or voltage source doesn’t matter.
2. Then find $R_{th}$ using Ohm’s law.

For a mix of independent and dependent sources:

1. First determine $V_{oc}$ across the terminals.
2. Then short-circuit the terminals and calculate $I_{sc}$. Remember to skip resistors where necessary (i.e., current takes path of least resistance, so short > resistor if in parallel).
3. Calculate $R_{th}$ with the voltage and current formula above.

AC analysis

For phasor analysis, Thevenin’s and Norton’s theorems still holds. Instead of a resistor, we have some impedance. Similar to the time domain, we have ${\text{V}}_{oc}$ and ${\text{I}}_{sc}$. Same relations as before.

See also

• Maximum power transfer, an application of the theorem