Polar coordinates

Polar coordinates (also called $r-\theta$ or modulus-argument) is a 2D coordinate system composed of two parameters: a modulus $r$ and a polar angle $\theta$ (with respect to the $x$-axis). We can easily extend to 3D-space with cylindrical and spherical coordinates, which adds additional parameters.

$$r=\sqrt{x^2+y^2}$$ $$\theta =\arctan \frac{y}{x}$$

We can convert back to rectangular coordinates:

$$x=r\cos \theta$$ $$y=r\sin \theta$$

Double integrals

The differential element is $rdrd\theta$. Think about the extra $r$ as because $\theta$ is unitless so we need some kind of element to account for this. More formally, it’s the Jacobian.

The change of variables with polar coordinates is much simpler than the general case in double integrals. We sketch out the region of integration and determine what’s going on. The order of integration does matter, but in many cases it’s difficult to determine an expression for $\theta =f(r)$, so we usually integrate in the order $drd\theta$.

Going through the above is pretty tedious. We may want to use a transformation matrix for polar to rectangular coordinates:

$$\text{M}=\left[\begin{array}{ccc}\cos \theta & & -\sin \theta \\ \sin \theta & & \cos \theta \end{array}\right]$$

Calculus of curves

The tangent line at some point associated with $\theta$ is:

$$\frac{dy}{dx}=\frac{dy/d\theta }{dx/d\theta }$$

The area bound by a curve between ${\theta }_1$ and ${\theta }_2$ is (think of the area of a sector of a circle):

$$A={\int }_{{\theta }_1}^{{\theta }_2}\frac{r^2}{2}d\theta$$

Kinematics

We need a new set of unit vectors since we’re not discussing rectangular coordinates anymore. We define ${\text{e}}_r$ and ${\text{e}}_{\theta }$ in the direction of the modulus, and a perpendicular direction that the angle is changing towards.

$$\text{r}=r{\text{e}}_r$$ $$\text{v}=\dot{r}{\text{e}}_r+r\dot{\theta }{\text{e}}_{\theta }$$ $$\text{a}=(\ddot{r}-r{\dot{\theta }}^2){\text{e}}_r+(r\ddot{\theta }+2\dot{r}\dot{\theta }){\text{e}}_{\theta }$$

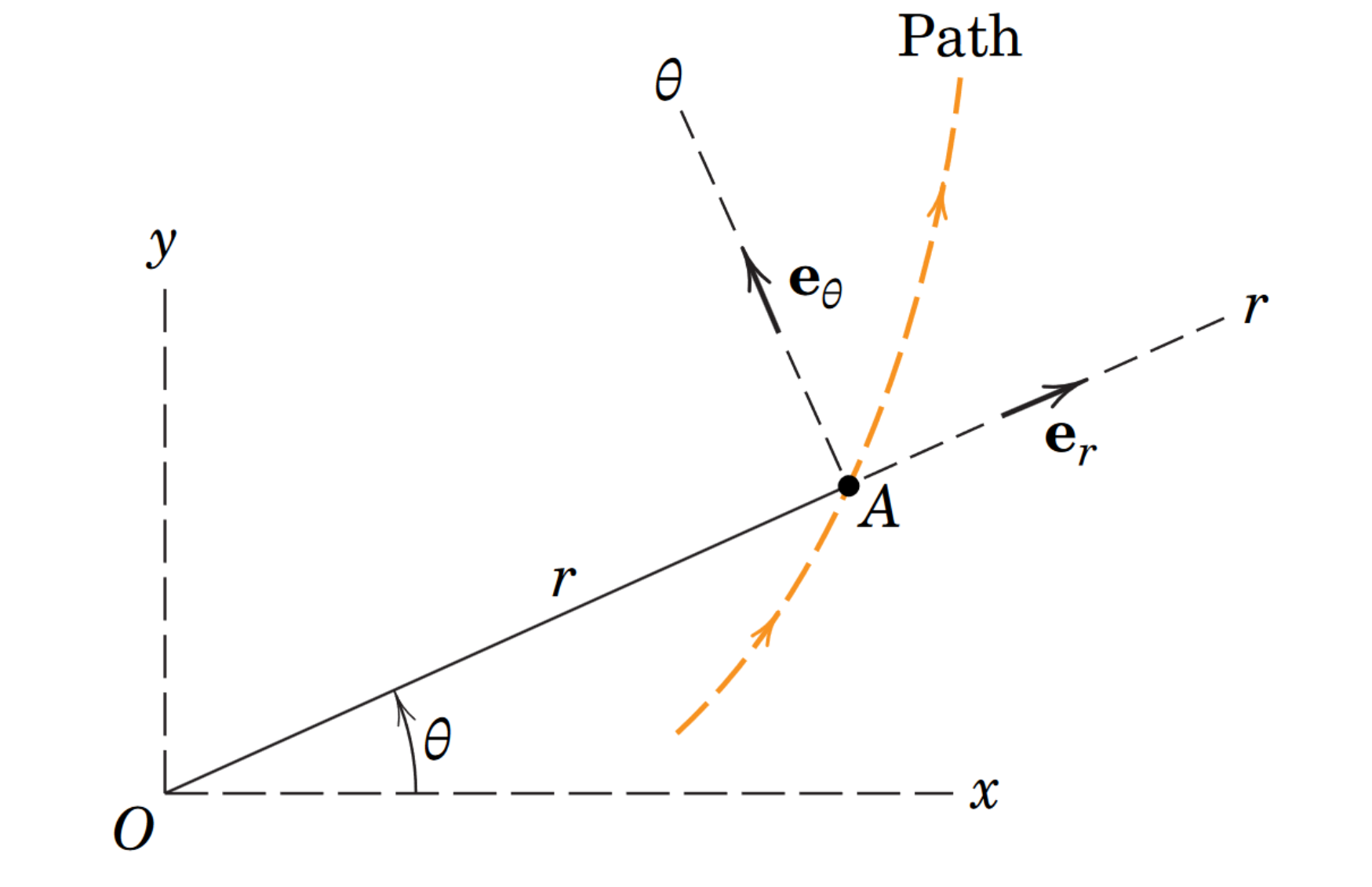
We often break these formulas apart into their constituent components, i.e., as follows.

$$a_r=\ddot{r}-r{\dot{\theta }}^2$$ $$a_{\theta }=r\ddot{\theta }+2\dot{r}\dot{\theta }$$

See also

For an extension to ${\mathbb{R}}^3$, see:

• Cylindrical coordinates
• Spherical coordinates