Spherical coordinates

We extend polar coordinates from ${\mathbb{R}}^2$ to ${\mathbb{R}}^3$ with spherical coordinates. We keep our radial distance $r$, polar angle $\phi$, and a new azimuthal angle 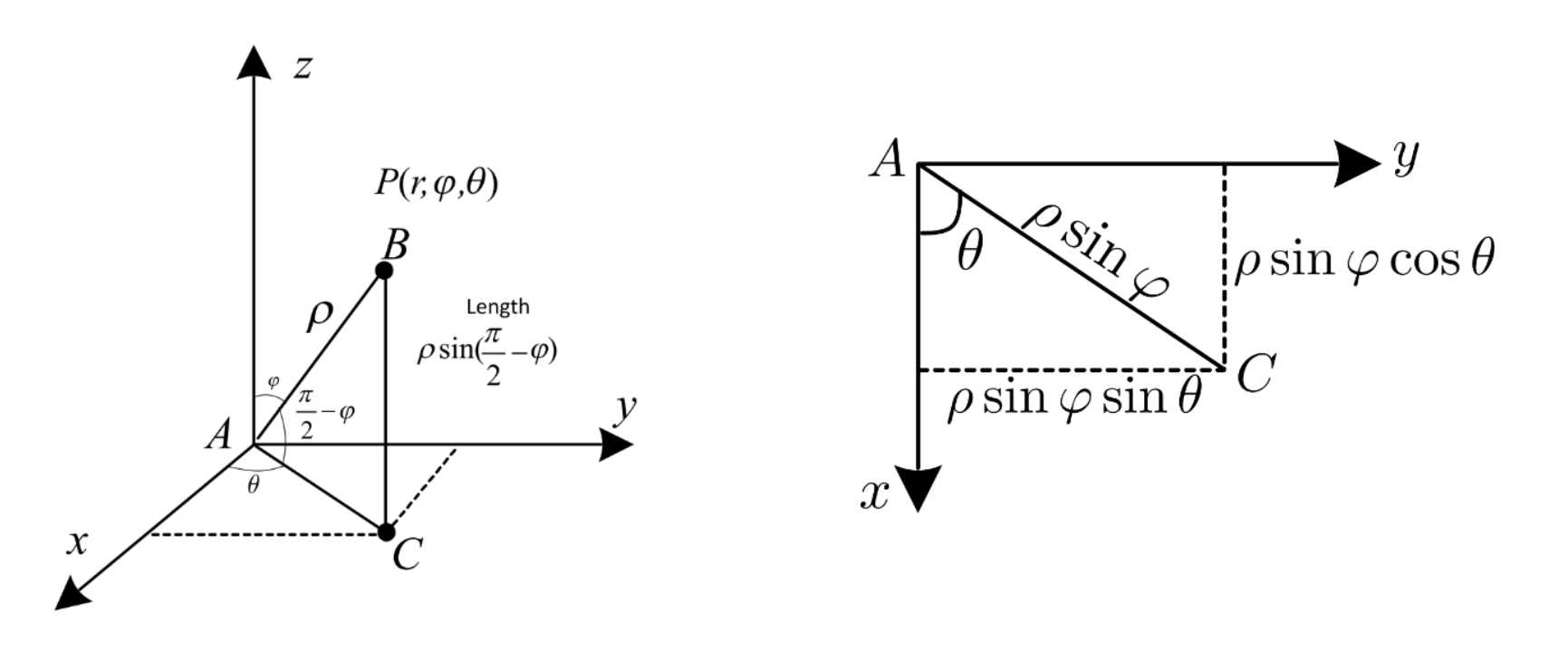$\theta$. Something immediate is that $\theta \in [0,\pi ]$ and must be in this interval. Our fundamental conversions are:

$$\rho =x^2+y^2+z^2$$ $$x=\rho \sin \theta \cos \phi$$ $$y=\rho \sin \theta \sin \phi$$ $$z=\rho \cos \theta$$

And the differential element is: ${\rho }^2\sin \theta d\rho d\theta d\phi$.

Triple integration

Similarly to polar and cylindrical coordinates, it’s difficult to understand intuitively what a function $\phi =f(\rho ,\theta )$ actually geometrically means, so it’s a good idea to do $d\rho d\theta d\phi$ as the order of integration. Questions where changing bounds is necessary means this is unavoidable, but we could be able to maintain bounds if they are still functions of outer bounds.

Quick conversions

It’s hard to intuitively get how to convert from a spherical to rectangular form (and vice versa), mainly because of the complicated trig functions. The move might be to just memorise this.

For a sphere with radius $a$ and a centre at the origin:

$$\rho =a$$

For a cone:

$$\phi ={\phi }_0$$

For a horizontal plane above and below the $xy$-plane at $z=\pm a$:

$$\rho =a\sec \phi ;\phi \in [0,\frac{\pi }{2}]$$ $$\rho =a\sec \phi ;\phi \in [\frac{\pi }{2},\pi ]$$

For a cylinder with radius $a$:

$$\rho =a\csc \phi$$

For a sphere with radius $a$ and a centre at $(0,0,a)$:

$$\rho =2a\cos \phi$$

Addendums

We have a transformation matrix for converting from spherical to Cartesian coordinates:

$$\text{M}=\left[\begin{array}{ccccc}\cos \theta \sin \phi & & \cos \theta \cos \phi & & -\sin \theta \\ \sin \theta \sin \phi & & \sin \theta \cos \phi & & \cos \theta \\ \cos \phi & & -\sin \phi & & 0\end{array}\right]$$

Occasionally we will see $\phi$ and $\theta$ swapped with each other. This is apparently a point of contention and you’ll see inconsistent definitions across textbooks and resources. $r$ is often swapped out for $\rho$ as well, but this can sometimes conflict with the symbol for density.

See also

• Cylindrical coordinates