Coulomb's law

In electromagnetism, Coulomb’s law describes the electrostatic force exerted by charged particles on each other. The direction of the force vectors depends on the sign of the charges. Recall: opposite charges attract, like charges repel.

$${\vec{F}}_{12}=\frac{1}{4\pi {ϵ}_0}\frac{q_1{q}_2}{\Vert {\vec{r}}_2-{\vec{r}}_1{\Vert }^3}({\vec{r}}_2-{\vec{r}}_1)$$ $${\vec{F}}_{12}=k\frac{q_1{q}_2}{\Vert {\hat{r}}_{12}{\Vert }^2}{\hat{r}}_{12}$$ $$k=\frac{1}{4\pi {ϵ}_0}=8.99\times 10^9\frac{N\cdot m^2}{C^2}$$

where $k$ is the electrostatic constant, ${ϵ}_0$ is the dielectric permittivity of free space, $q_i$ is the respective charge of each particle. The direction of the force is determined by the unit vector ${\hat{r}}_{12}$, which points from charge 1 to charge 2. The first and second statements of the law are equivalent, but the first is easier because it avoids a unit vector conversion.

The forces follow the principle of superposition. For a system of charges, we need to find all net force relations, i.e., for a system of three charges, we need three equations with two terms each.

$${\vec{F}}_{1,net}=\sum _i^n\overrightarrow{F_{1,i}}$$

We can relate to the electric field:

$$\frac{\vec{F}}{q}=\vec{E}$$

Calculations

A helpful representation is to give $\hat{r}$ in terms of spherical coordinates:

$$\hat{r}=\cos \phi \sin \theta \hat{x}+\sin \phi \sin \theta \hat{y}+\cos \theta \hat{z}$$

where $\theta$ is the azimuthal angle (with respect to the $z$-axis) and $\phi$ is the polar angle. Why spherical though? Because the electrostatic force is spherically symmetrical for all possible values of $\theta$ and $\phi$, i.e., it only depends on the distance $\Vert \hat{r}\Vert$.

Formal statement

For two point charges $q_1$ and $q_2$, we want to first define the distance vector between them. From the origin of the coordinate system, we define ${\vec{r}}_1$ and ${\vec{r}}_2$. Then, ${\vec{r}}_{12}$ is defined as the vector originating from $q_1$ pointing to 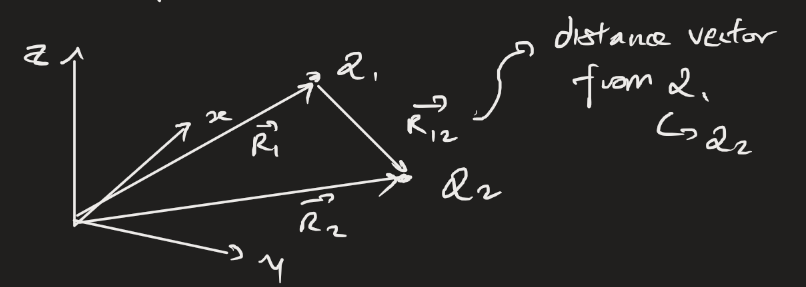$q_2$. Then, the force from $q_1$ to $q_2$ is given by ${\vec{F}}_{12}$.

$${\vec{F}}_{12}=\frac{1}{4\pi {ϵ}_0}\frac{q_1{q}_2}{\Vert {\vec{r}}_2-{\vec{r}}_1{\Vert }^3}({\vec{r}}_2-{\vec{r}}_1)$$

If we express in terms of the unit vector:

$${\hat{r}}_{12}=\frac{{\vec{r}}_{12}}{\Vert {\vec{r}}_{12}\Vert }$$

Substituting in will simplify the statement of the law, and prove that it’s still an inverse square law. Note the similarity to Newton’s law of gravitation.