Red-black tree

A red-black tree is a data structure that functions as an approximately height-balanced binary search tree. There are key red-black properties we must satisfy:

• Every node is either red or black (i.e., a colour attribute)
• The tree’s root node is black. Subtrees need not follow this restriction.
• Every leaf (a nullptr value) is black.
• If a node is red, then both of its children are black.
• For each node, all simple paths from the node to descendant leaves contain the same number of black leaves.

We also define the black height of a node $x$ as $\text{bh}(x)$, the number of black children to a leaf excluding $x$ itself. By the final property, this is well-defined and consistent.

For search, we maintain similar runtime complexity as BSTs, $\mathcal{O}(\log n)$, while avoiding the worst-case of $\Omega (n)$. As with other trees, we maintain a space complexity of $\mathcal{O}(n)$.

Rotations and insertions

The mechanism by which red-black trees maintain height balance is via rotations. Notably, rotations preserve the binary search tree property. This is best understood geometrically: the root of the new subtree will be modified. 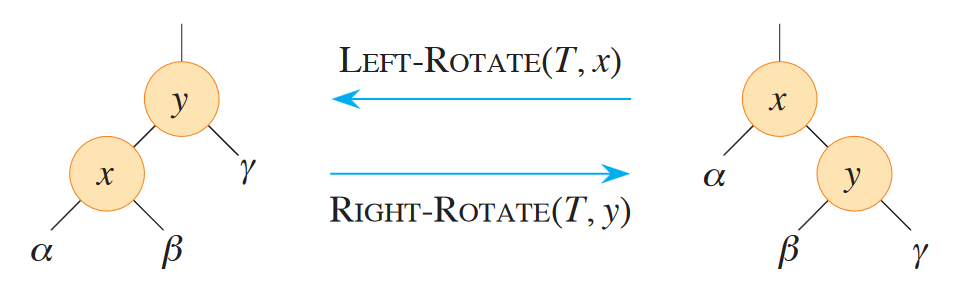Rotations are used when inserting a node into red-black trees. We insert the node just like we do with BSTs, and initially colour it red. Then, we check the resulting subtree to see if it violates the red-black properties. If it does, we perform certain manipulations.

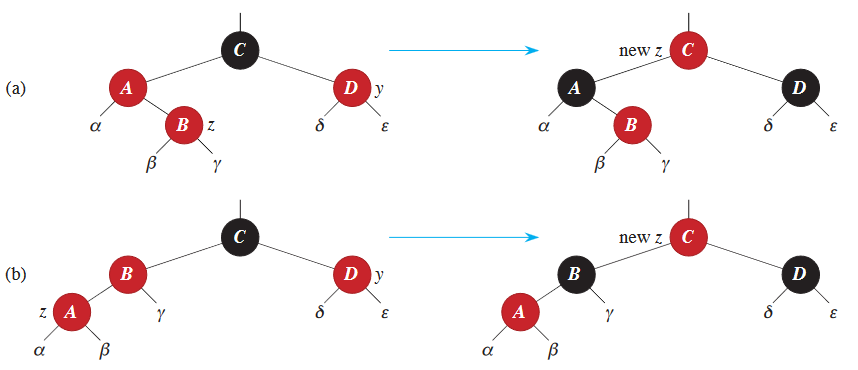
There are three main rotation cases when we insert a red node $z$. In the first case, the sibling node of $\text{parent}(x)$ is red (because of property 4, parent is also red). In this case, we push the blackness of the grandparent node down to the parent and uncle nodes. Then, the grandparent node becomes red. Then, we switch the new node $z$ with the grandparent.