Least squares

Least squares is a method used to build regression models. An easy way to apply it is through matrix multiplication. We can use it to build simple and multiple linear regression, as well as polynomial regression models.

The premise

Given some points that may not be colinear, we may be faced with finding a solution that minimises the error (residual sum of squares) between a regression line and the points. This minimiser is called a least-squares solution.

Let’s use an example in an attempt to make this concrete. Say we have the points $(1,2)$, $(2,5)$, and $(3,6)$, where we have a linear system of equations. We attempt to find some coefficient $c_0\ast$ for the constant term, and $c_1\ast$ for the term with degree 1. We set $A$ as the matrix we multiply the coefficient vector by.

$$\left[\begin{array}{cc}1& 1\\ 1& 2\\ 1& 3\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\end{array}\right]=\left[\begin{array}{c}2\\ 5\\ 6\end{array}\right]$$

From projections, we use the theorem:

Suppose $V$ is a subspace of ${\mathbb{R}}^n$ and $\vec{x}\in {\mathbb{R}}^n$. The closest vector in $V$ to $\vec{x}$ is given by ${\text{Proj}}_V(\vec{x})$. In other words, $\Vert {\text{Proj}}_V(\vec{x})-\vec{x}\Vert \le \Vert \vec{v}-\vec{x}\Vert$ for any $\vec{v}\in V$.

In other words, the least-squares solution is given by the projection onto the column space of $A$.

The formula

For some matrix $A$, and some vector $\vec{b}$, we apply the following formula to obtain coefficient terms. This example gives us linear terms, but we can easily extend this to find higher degree terms (i.e. quadratic terms).

$${\vec{x}}^{\ast }=(A^{T}A{)}^{-1}{A}^T\vec{b}$$ $$A{\vec{x}}^{\ast }=A(A^{T}A{)}^{-1}{A}^T\vec{b}$$

Applications

Two-dimensional models

We can extend this to a much larger data set, as follows, where we’re building a simple linear regression model in 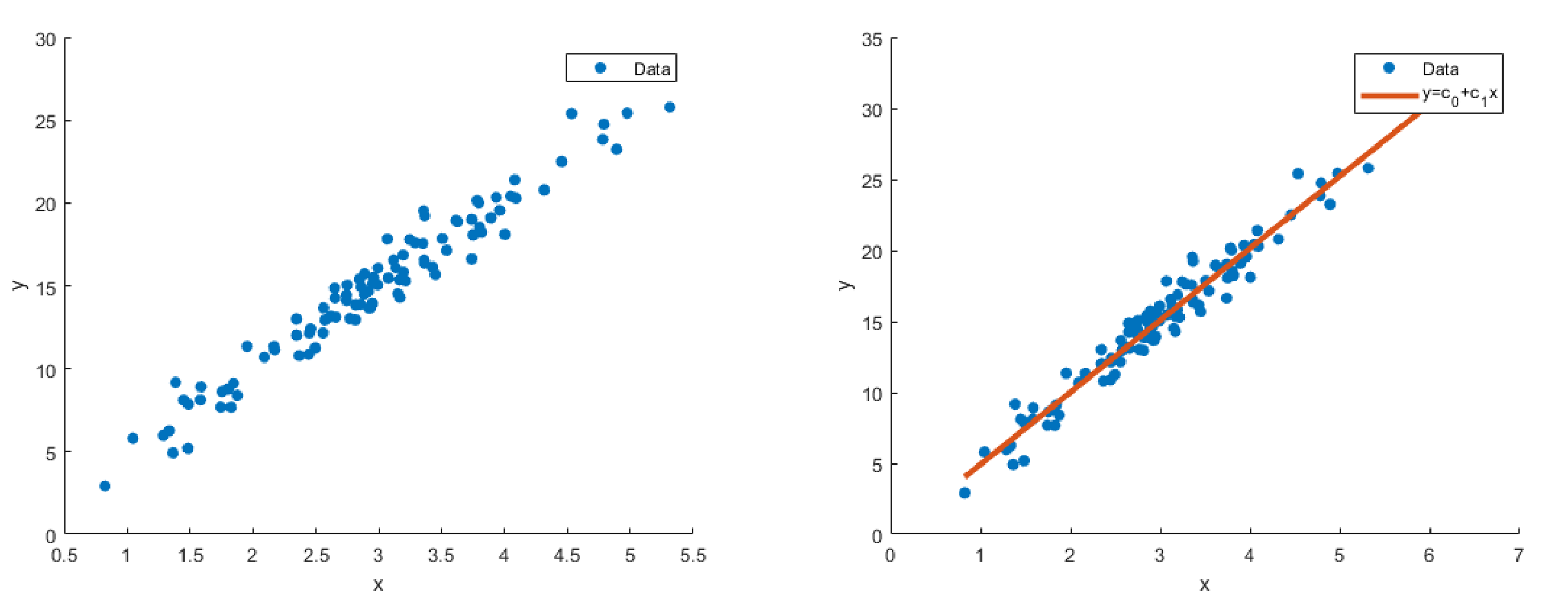${\mathbb{R}}^2$. When we’re building our matrix $A$, we have the first column (for $c_0$, the coefficient of degree 0) as entirely ones. Our independent variable should be the second column (unchanged, for $c_1$ degree 1). As we continue with higher-order polynomial regression models, we should correspondingly take the independent variable to the n-th exponent correspondingly (i.e., for $c_3$, we cube the independent variable for the fourth column).

data = table2array(data);
A_0 = [ones(length(data), 1)]; % 0-order sets the first column as entirely ones
A_1 = [A_0, data(:, 1)]; % 1-order, sets the second column as ind. variable
 
for i = 1:height(data) % 2-order, squares the ind. variable
	data(i, 3) = data(i, 1)^2;
end
 
A_2 = [A_1, data(:, 3)];
c_2 = inv(transpose(A_2) * A_2) * transpose(A_2) * data(:, 2);
% builds coefficient vector

Multi-dimensional models

Least squares can also build multiple linear regression models, where we examine the linear relationship between multiple variables.

data = table2array(diabetes_data);
A = [ones(length(data), 1), data(:, 1:10)] % takes the first 10 columns of the data
c = inv(transpose(A) * A) * transpose(A) * data.Y; % where Y is our target vector b

See also

• Pearson correlation coefficient, a metric we use to determine correlation of linear data