Linear equation

A linear equation is an equation of the form:

$$a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n=b$$

We often examine systems of linear equations, where we have multiple linear equations and are asked to determine whether there is a corresponding solution. To do this, we use row reduction or Cramer’s rule.

Systems of equations can be encoded in matrices:

$$\left[\begin{array}{c}x+2y+3x=39\\ x+36+2z=34\\ 3x+2y+z=26\end{array}\right]\to \left[\begin{array}{ccc}1& 2& 3\\ 1& 36& 2\\ 3& 2& 1\end{array}\right]\vec{x}=\left[\begin{array}{c}39\\ 34\\ 26\end{array}\right]$$

We can only interpret our results geometrically in ${\mathbb{R}}^3$ or under, but the general idea is similar as we extend past three dimensions. Our results vary between a unique solution, infinitely many solutions, and no solution at all, in the respective images below.¹ In other words, we determine the nature of the intersection of the lines, planes, or higher-dimensional objects by solving these systems. 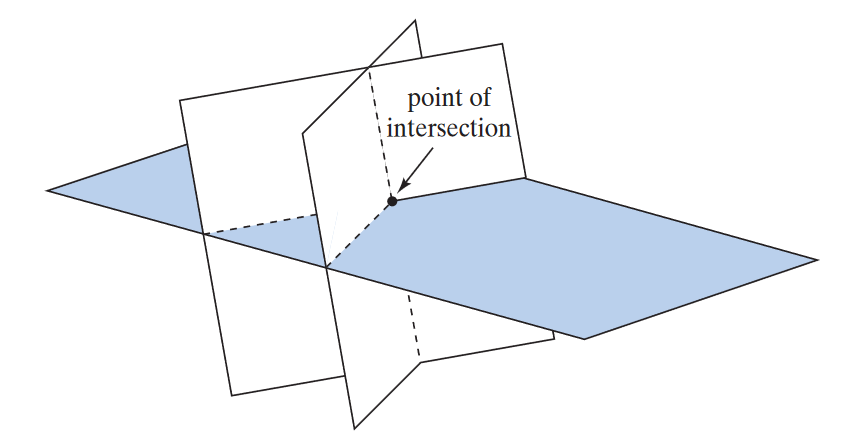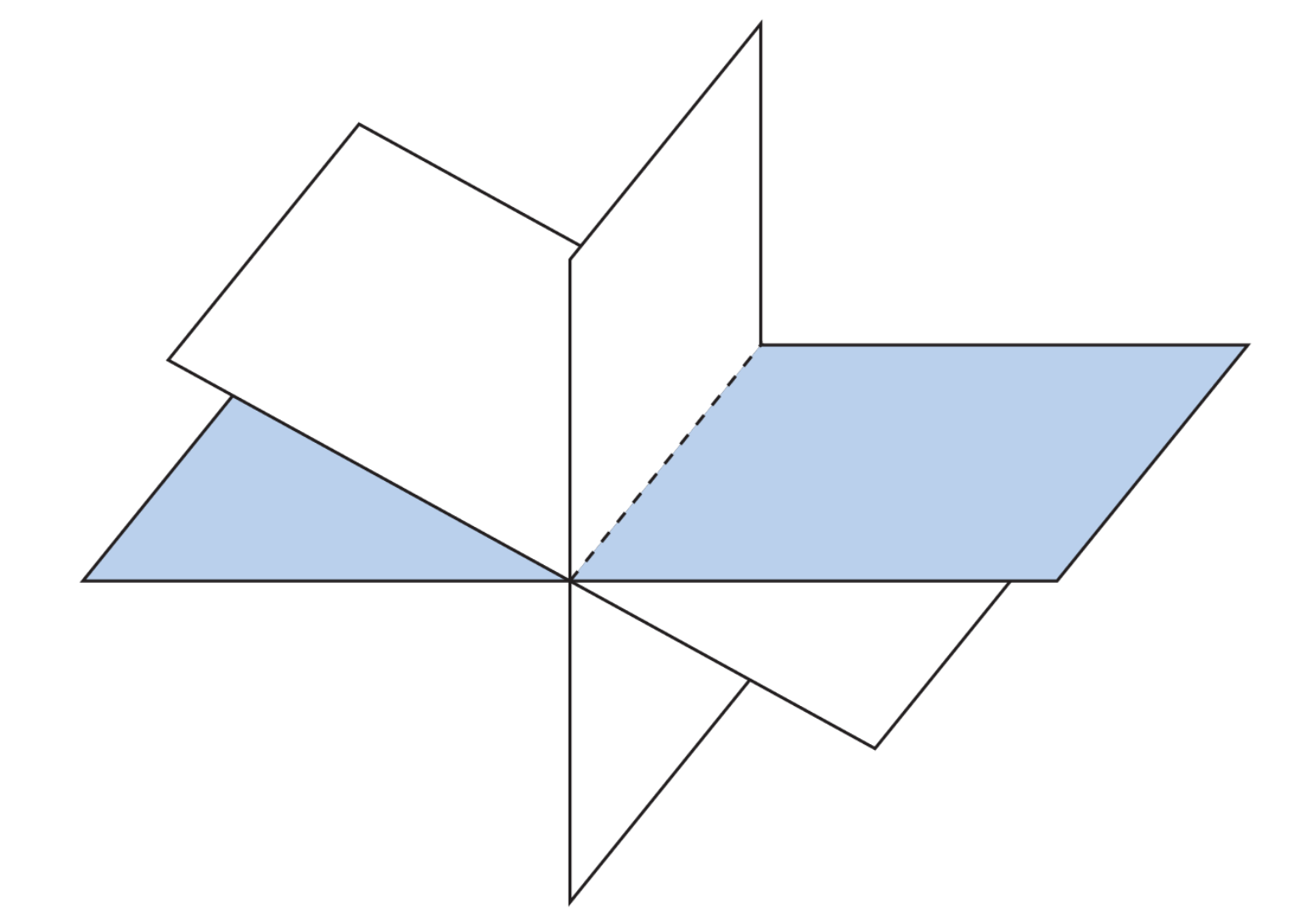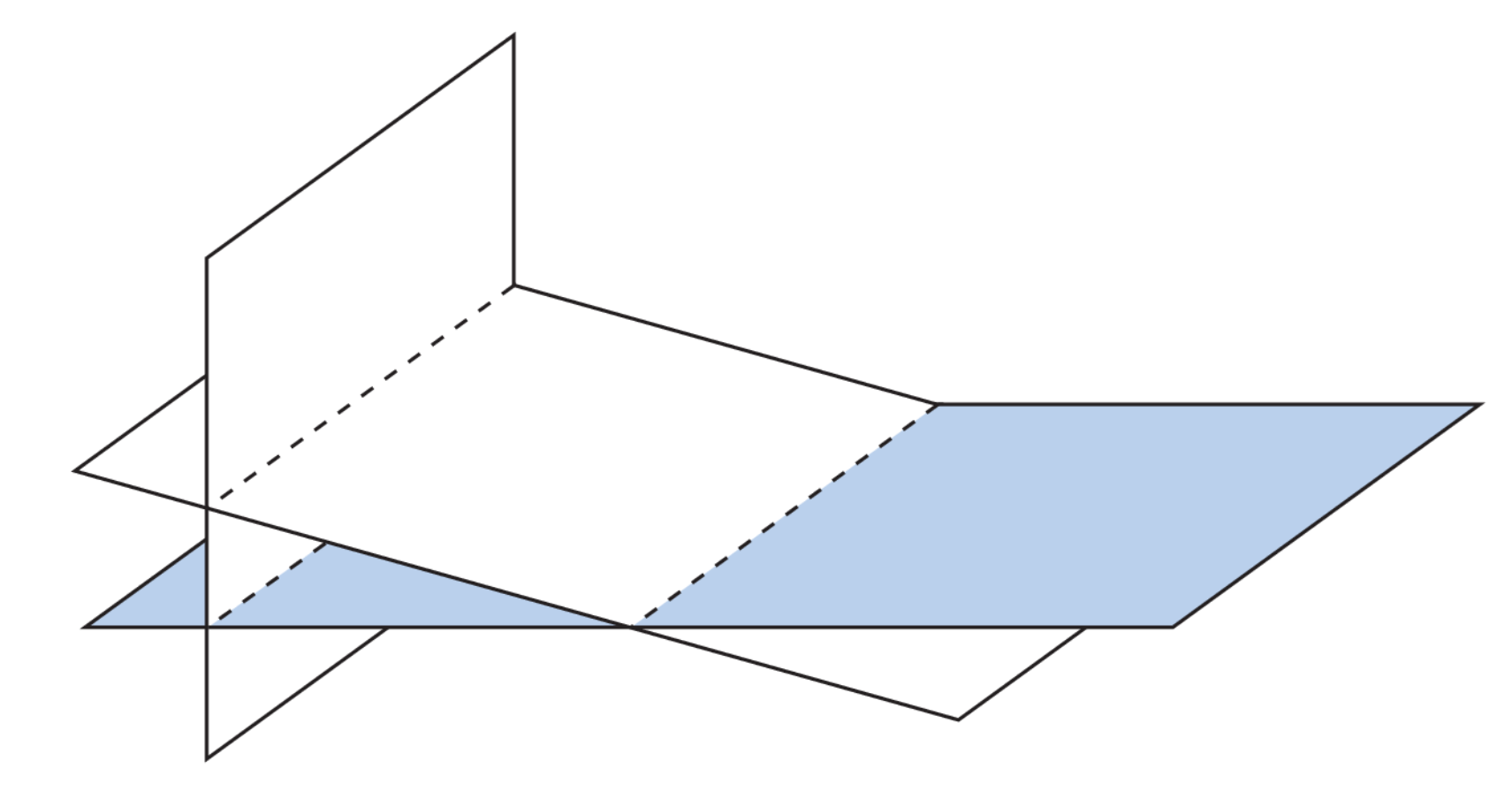We refer to systems with no solutions as inconsistent.

See also

• Line
• Plane

Footnotes

1. From Linear Algebra with Applications, by Otto Bretscher. ↩