Mesh analysis (also loop analysis) is an analysis method used to solve linear circuits. This method only works for planar circuits, where the branches don’t overlap. There should be a total of linearly independent KVL equations, or alternatively .
In general, we try to avoid loops with current sources and instead set-up supermeshes. Current sources will describe the current of a given mesh very easily — so they’re still very convenient for our analysis.
The setup
For each “window”, we assign a clockwise current loop, . When two mesh currents go through the same element they go through it in opposite reference directions.
We can systematically create KVL equations pretty quickly. For some AC or DC loop, we:
- Multiply the loop current by the sum of the resistances in the loop.
- Subtract any shared resistances multiplied by the loops they’re shared with.
For example:
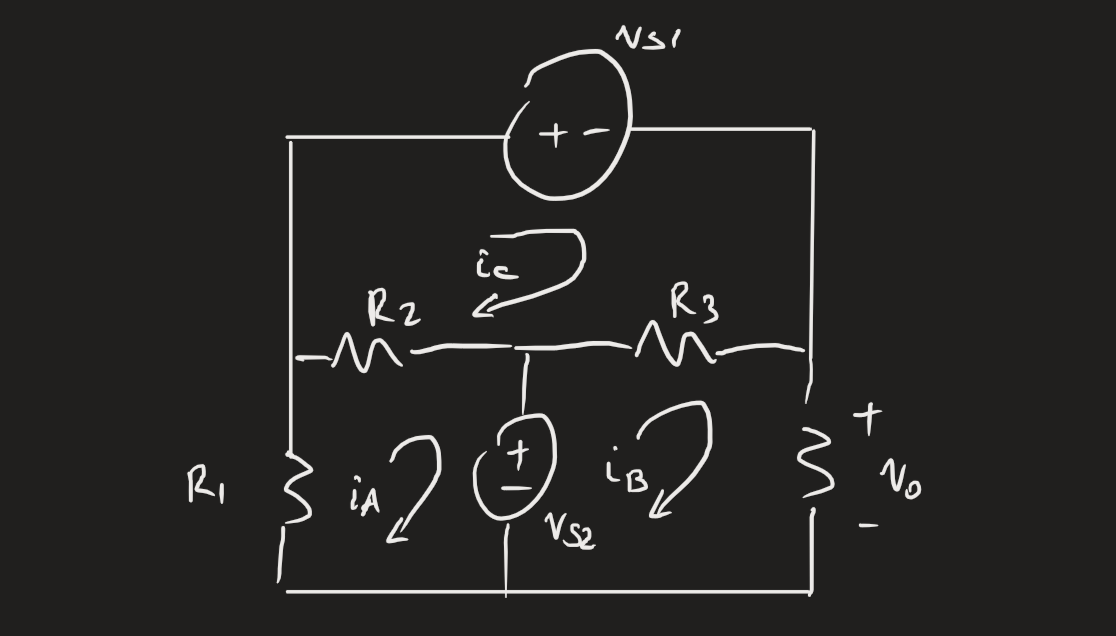This circuit has the following equations:
And so on. Note that if the current exits the voltage source’s positive terminal, we set it as positive on the other side of the equation, and vice versa.