Biot-Savart law

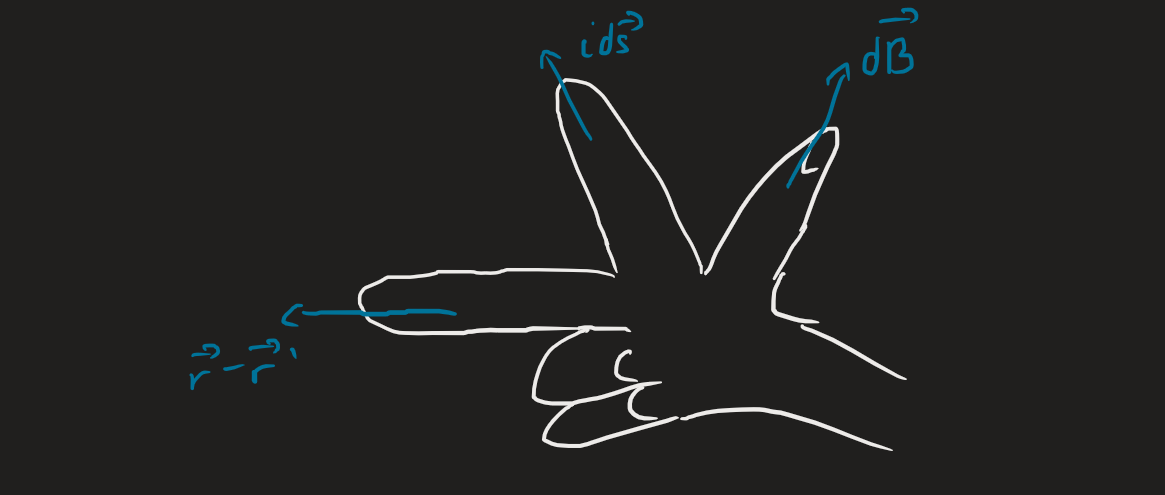
The Biot-Savart law gives an expression for the net magnetic flux density ($\vec{B}$) at a point due to a current through a differential length element.

$$d\vec{B}=\frac{\mu }{4\pi }\frac{id\vec{l}\times (\vec{r}-{\vec{r}}^{\prime })}{\Vert \vec{r}-{\vec{r}}^{\prime }{\Vert }^3}$$

where $\mu$ is the magnetic permeability constant (often of free space). To calculate the total magnetic field, we integrate over the wire.

Using the right-hand rule, we can determine the direction of $\overrightarrow{dB}$.

Computations

To find the magnetic flux density, we take several steps that are very similar to our computation of the electric field.

1. Choose an applicable coordinate system.
2. Pick an arbitrary differentially small length element, and determine an expression for $id{\vec{l}}^{\prime }$.
3. Find the resulting expression for $d\vec{B}$.
4. Integrate over a suitable integral.

As always, ${\vec{r}}^{\prime }$ points to the source, and $\vec{r}$ points to the observation point.

Simple geometry

For a long straight wire:

$$B=\frac{{\mu }_{o}i}{2\pi R}$$

For a semi-infinite straight wire:

$$B=\frac{{\mu }_{0}i}{4\pi R}$$

At the centre of a circular arc with angle $\phi$ (we can use this to derive the other formulas):

$$B=\frac{{\mu }_{0}i\phi }{4\pi R}$$