Time value of money

A basic principle in finance and in economics is the time value of money (TVM). It’s the idea that we cannot directly compare $1todaywith$1 to be received in the future. This is mainly because the value of money changes (usually due to inflation) over time, so $1inthefutureoftengetsyoulessthan$1 in the present.

The compounding rate (also discount rate or required rate of return) is the variable that equates today’s present value with a later date’s future value.

$1(1 + i)^n>$1 $$PV=\frac{FV}{(1+i{)}^n}$$

The key implication of this idea is that when we deal with money, both the magnitude and the timing matter. If someone is indifferent between receiving some base sum today (say 1000) and some future sum (\X), then $X has a present value of $1000 for that person (i.e., the time value of money is subjective).

This change in value is primarily because of interest. If $i=0$, then we don’t consider TVM.

Computations

For a single sum of money, we use the equation:

$$PV=\frac{FV}{(1+i{)}^n}$$

i.e., where we have a single sum at some time, make no additions or withdrawals, and then we just want to know what the future value is.

We commonly denote this compounding factor with a special notation.

$$(F|P,i,n)=(1+i^n)$$

And the discount rate is denoted with:

$$(P|F,i,n)=(1+i{)}^{-n}$$

Both values can be found using a look-up table (in ECE472 — Engineering Economic Analysis and Entrepreneurship). Note that we use discrete values because they’re used in business for a finite period.

For the present value of a series of $n$ cash flows, we have:

$$PV=A_0+\sum _{k=1}^n{A}_k(P|F,i,k)$$

And accordingly, for the future value of a series of $n$ cash flows, we have:

$$FV=A_0(1+i{)}^n+A_1(1+i{)}^{n-1}+\cdots +A_n=\sum _{k=0}^n{A}_k(F|P,i,n-k)$$

Series of cash flows

A uniform series of cash flows (also called an annuity) has a closed form summation:

$$PV=\sum _{k=1}^{n}A(1+i{)}^{-k}=A\left[\frac{(1+i{)}^n-1}{i(1+i{)}^n}\right]$$ $$A_k=A$$

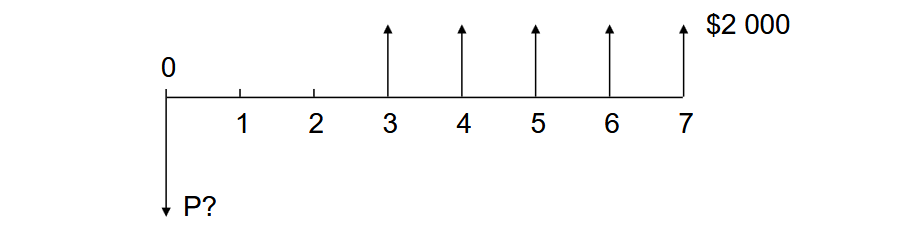
A gradient series has each successive cash flow increase by a fixed amount equal to 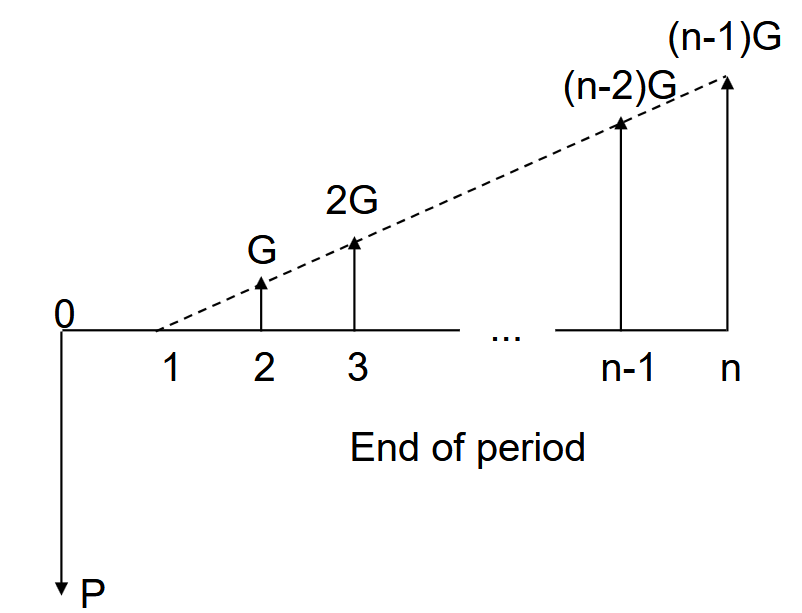$G$. Like before, the summation has a closed form:

$$P=G\left[\frac{1-(1+ni)(1+i{)}^{-n}}{i^2}\right]$$