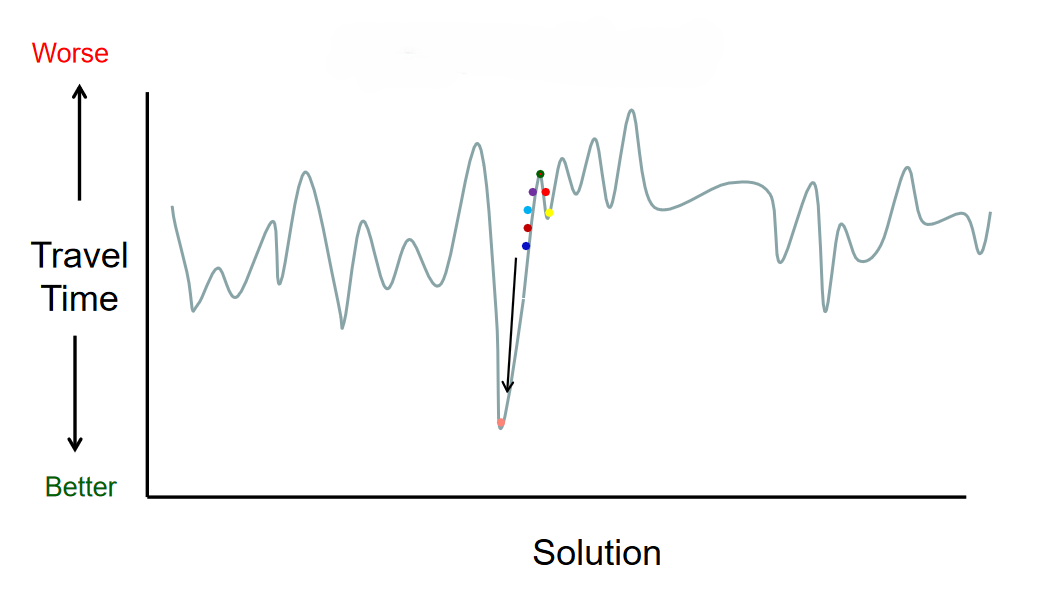
Simulated annealing is a local search algorithm that aims to reach the best local minimum by mimicking the physical process of annealing. It’s a version of stochastic hill climbing where some bad moves are allowed. When metals are annealed, they cool slowly, and atoms gradually move to a lower energy state resulting in a stronger/more optimal material.
In simulated annealing, we start with a poor initial solution and high temperature . We then perturb the solution: SA will pick a random move (hence the stochasticity) instead of the best move. We perturb frequently to “shake” just hard enough that the solution falls out of the local minimum into a better local minimum.
If the move improves the solution, it will always be accepted. If it doesn’t, there’s a probability that the move will be picked where most perturbations will be accepted if is high but only good ones will be accepted as . is often a Boltzmann distribution, i.e., it decreases exponentially with the “badness” of the move (i.e., by the amount by which the solution quality is worsened) and with the temperature’s decrease.