Stochastic gradient descent (SGD) is a variant of gradient descent where each iteration evaluates the gradient at a random point. In the context of machine learning, this evaluates a random training sample set (a minibatch of examples) from the dataset. SGD is used in nearly all of deep learning.
This generally results in an optimisation path that may look erratic, but can perform more of a global search for the best optimum, resulting in better model parameters (i.e., weights). Its reduced computational cost over regular gradient descent is also preferable, because it relies on an estimate instead of a symbolic calculation.
Strictly speaking: if we use SGD, we update weights (number of iterations in each epoch) with the same number of examples in the training set. If we use minibatches, we do number of iterations. Batch gradient descent does it a single time.
Variants
Since the search space can include some “ravines” (common around local optima), SGD can have some trouble navigating this space, and will oscillate across the slopes of the ravine. This motivates using “momentum” to accelerate SGD in a relevant direction while dampening oscillations.
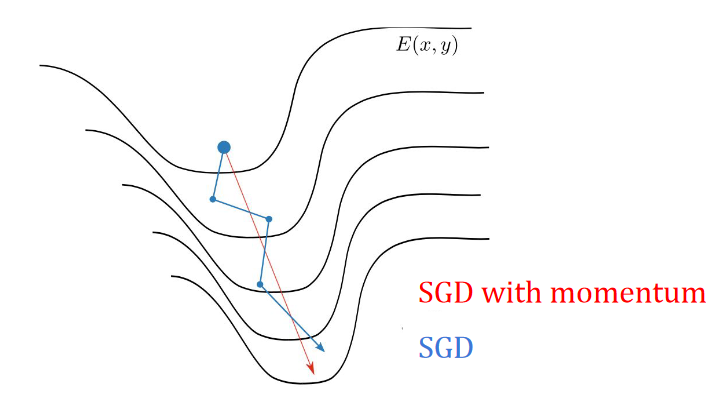This momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. We reach a terminal velocity defined by:
tocheck wtf is this How can we keep the benefits of SGD with momentum, but to ensure the weights are adaptive? This motivates adaptive moment estimation.
In code
PyTorch supports SGD within the torch.optim class:
# import torch.optim as optim
optimiser = optim.SGD(model.parameters(), lr=0.05, momentum=0.9)See also
- Simulated annealing, a variant of stochastic gradient descent where some bad optimisations are accepted