Local search describes a broad category of algorithms that search from a start state to neighbouring states without keeping track of the paths nor the set of states that have been reached. This means that they are non-systematic and may never explore the entirety of the search space where a solution may be.
This carries two advantages: they use a small amount of memory and they can find reasonable solutions in large/infinite state spaces (like some NP-complete problems) where a systematic algorithm just won’t work. Some problems might not care about the path we take to get to the solution.
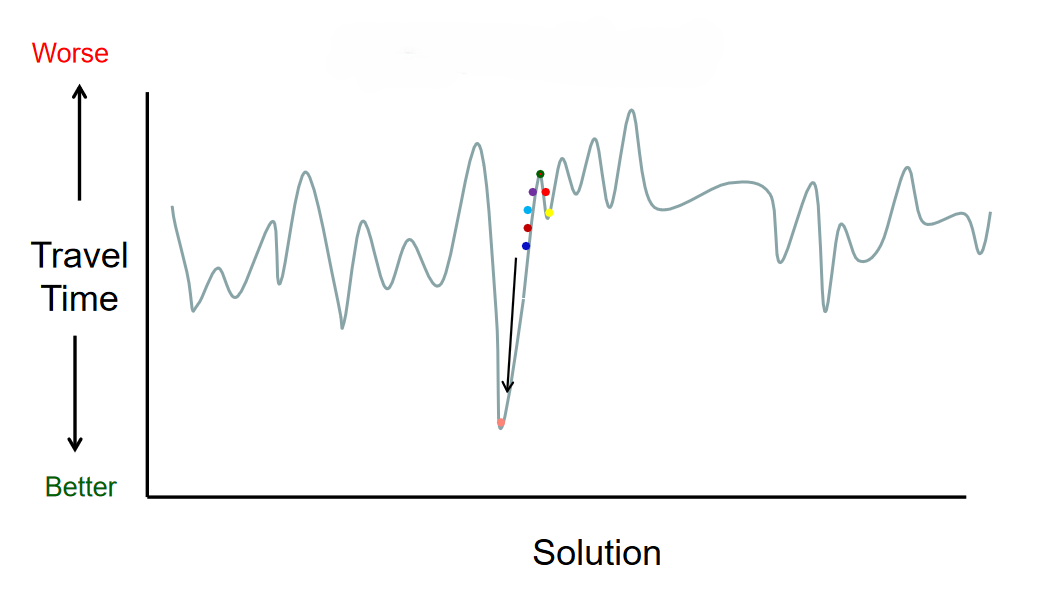
State spaces have a multidimensional possible set of solutions. We compare them against an objective function to see whether the solution is optimal. The goal is that we aim to optimise the solution. Note that we see many local maxima and minima. When the local search algorithm operates, it may only explore a small subset of the possible solution space, but get a reasonable solution. We want to find the global optimum (maximum or minimum) in an iterative process called gradient descent.