Nyquist stability criterion

In control theory, the Nyquist stability criterion gives us a visual way to determine the stability of feedback systems. It states that a feedback system is stable if and only if the contour ${\Gamma }_L$ in the $L(s)$ plane doesn’t encircle the $(-1,0)$ point when the number of poles in the right-hand $s$-plane is zero.

If the number of poles in the RHP is other than zero, the Nyquist is criterion is stated such that the system is stable if and only if the number of counter clockwise encirclements of the $(-1,0)$ point is equal to the number of poles with positive real parts.

Procedure

We convert a Nyquist contour ${\Gamma }_s$ from the $\sigma -j\omega$ plane into the $L(s)$ pla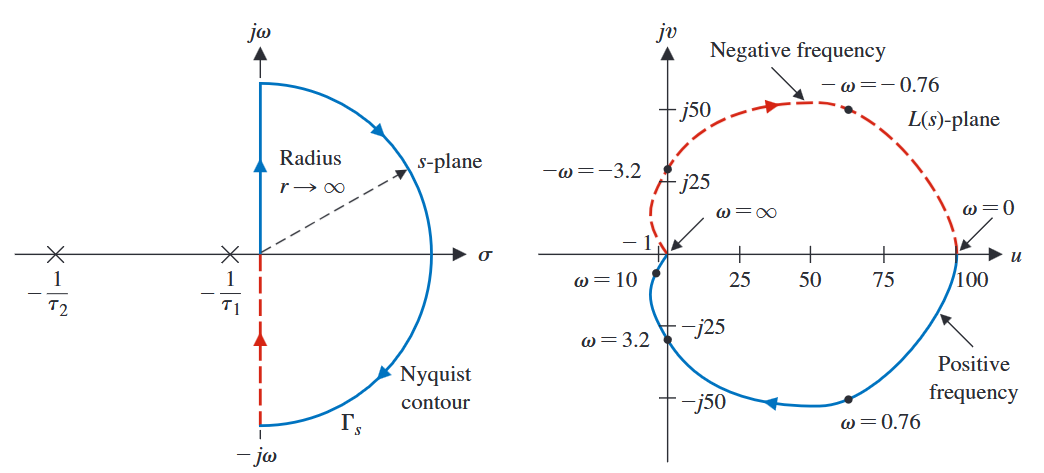ne: The function we operate on is the $P(s)C(s)$ function, or the product of the plant and the controller. If $G(s)$ has no poles nor zeroes on $D$, then the Nyquist plot encircles the origin exactly $n-m$ times CCW. This holds for $\text{Re}(s)\ge 0$.