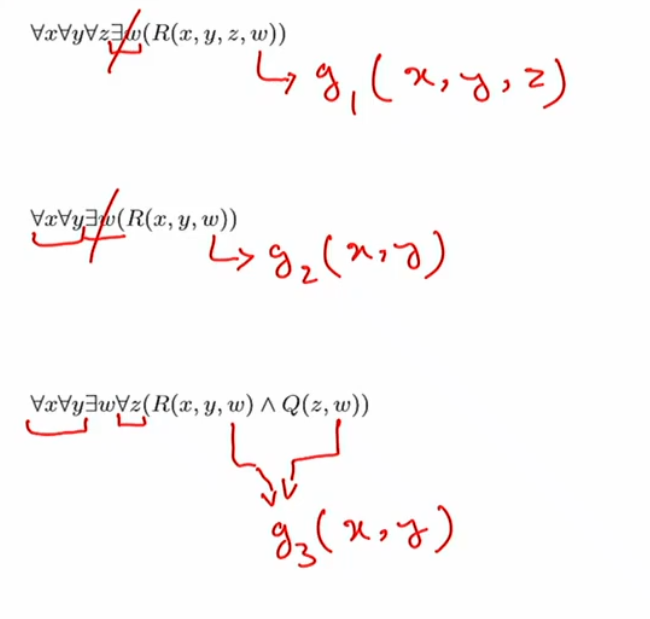Resolution

Resolution works with formulas expressed in clausal form:

• A literal is an atomic formula or the negation of an atomic formula.
• A clause is a disjunction of literals.
• A clausal theory is a set of clauses.

basically:

• if $c$ is false, then $a_1$ must be true
• if $\neg c$ is false, then $b_1$ must be true

first clause, second clause resolved together

$$Q(x,y)\vee R(y)$$

new clause is called the resolvant of the two clauses

contradiction: denoted by an empty clause $()$

The conversion to clausal form requires a list of steps:

• Eliminate implications.
  • $A\to B⟺\neg A\vee B$. Convert to the right form.
• Move negations inwards and simplify any double negations.
  • $\neg \neg A⟺A$
  • De Morgan’s laws
    • $\neg (A\wedge B)⟺\neg A\vee \neg B$
    • $\neg (A\vee B)⟺\neg A\wedge \neg B$
  • $\neg \forall xA⟺\exists x\neg A$
  • $\neg \exists xA⟺\forall x\neg A$
• Standardise variables. Here, we want to rename variables so that each quantified variable is unique. i.e., if two variables are named the same, but exist in non-conflicting scopes, then we should rename them such that they don’t conflict.
• Get rid of the existential quantifiers (also called skolemisation).
  • add function symbols that mention every universally quantified variable that scopes the existential
• Move all the quantifiers to the front. This converts to prenex form.
• Distribute conjunctions over disjunctions.
  • $A\vee (B\wedge C)⟺(A\vee B)\wedge (A\vee C)$
• Flatten nested conjunctions and disjunctions.
  • $A\vee (B\vee C)⟺(A\vee B\vee C)$
  • $A\wedge (B\wedge C)⟺(A\wedge B\wedge C)$
• Convert to clauses, by removing universal quantifiers and breaking apart conjunctions.