In deep learning, residual networks are a type of architecture used primarily to avoid the vanishing gradient problem in very deep networks. This is done by using “skip connections” to provide deeper layers’ gradient computations more direct access to signals that might otherwise be lost.
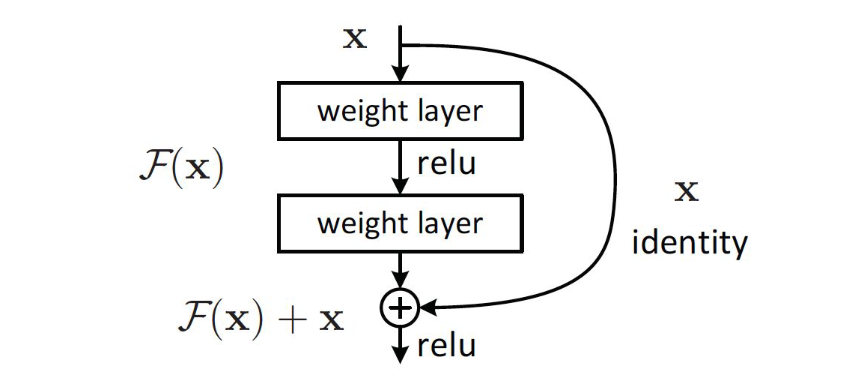One consideration: we need to make sure that the dimensions of and are consistent. Oftentimes if we simply apply a pooling layer this can result in inconsistent dimensions. To rectify this, we may be interested in applying a linear transformation .
Original paper
In the original paper, sizes were downsampled using a stride=2 instead of max/average pooling. After the last convolutional layers, we use global average pooling, meaning the embedding has no spatial dimension and only consists of 512 floats.
Meaning: our CNN is input-dimension invariant. Previously, we had to standardise the dimensions of the input because we hardcoded the dimension changes.
At the end, all we need is a single fully-connected classification layer, because the learned embeddings are so good we don’t need a complex classifier at the end of the model.
In code
# normal layer
next_activation = layer(activation)
# residual layer
next_activation = activation + layer(activation)