Normal-tangential coordinates

Normal-tangential coordinates (also $n-t$ coordinates), are defined by a tangential and a normal component to movement.

Unit vectors

We introduce two unit vectors: ${\text{e}}_n$ in the normal direction, and ${\text{e}}_t$ in the tangential direction.

$${\text{e}}_t=\vec{T}(t)=\frac{{\vec{r}}^{\prime }(t)}{\Vert {\vec{r}}^{\prime }(t)\Vert }$$ $${\text{e}}_n=\vec{N}(t)=\frac{{\vec{T}}^{\prime }(t)}{\Vert {\vec{T}}^{\prime }(t)\Vert }$$

In ${\mathbb{R}}^2$, both the tangent and normal vectors can have two possible orientations. Questions will specify which orientation to consider. When we extend to ${\mathbb{R}}^3$, there are infinitely many normal vectors, so we don’t consider this case.

Visualisation

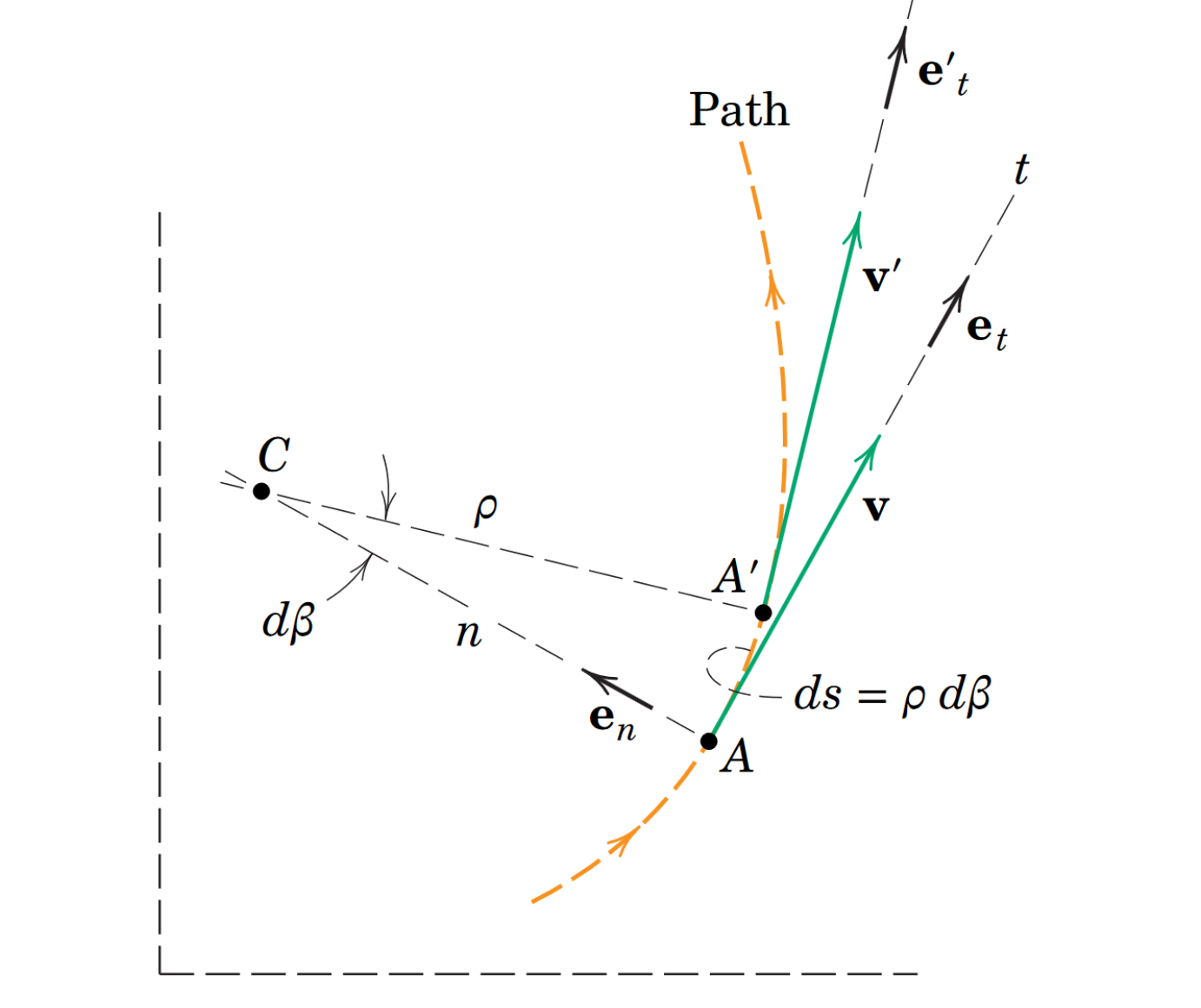
A more useful geometric interpretation comes from our understanding of vector-valued functions. The positive $n$ direction will always point towards the centre of curvature; if curvature changes direction, so too will the positive $n$-direction. At an inflection point, the normal acceleration goes to 0 because $\rho$ approaches infinity.

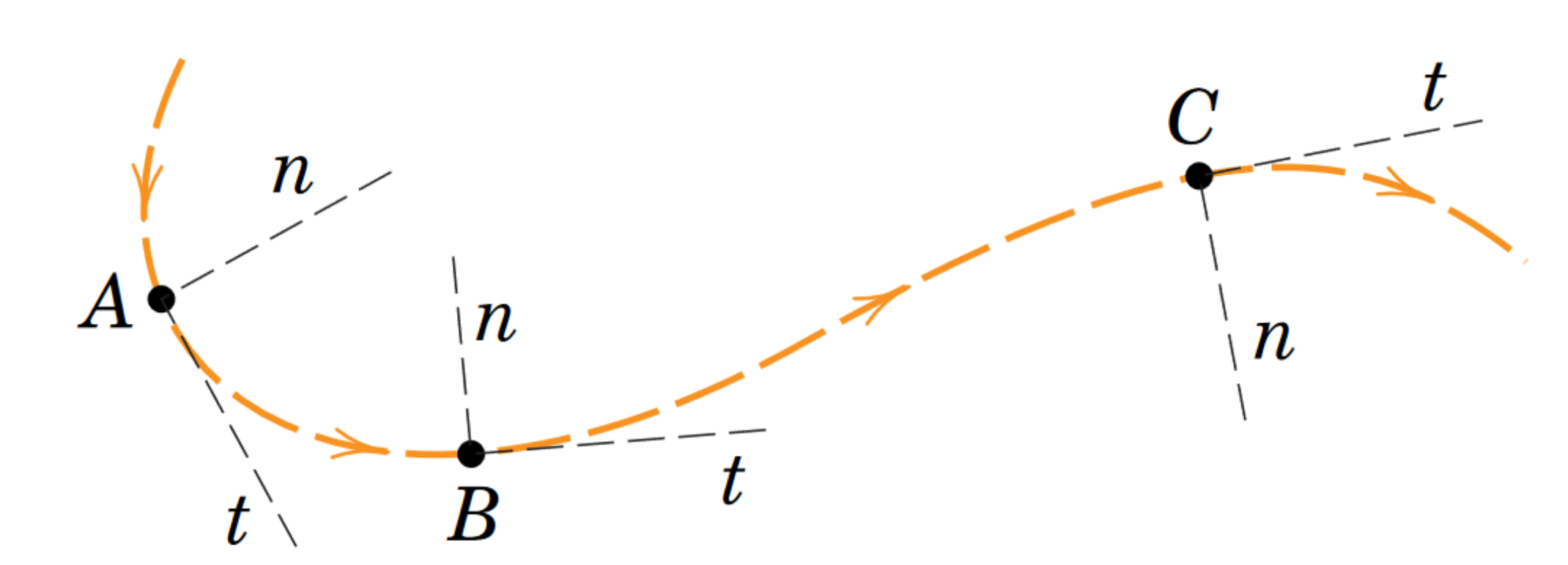
Kinematics

We can relate $n-t$ coordinates with $r-\theta$ coordinates in circular motion problems. We can’t express displacement in $n-t$ coordinates, but we can express velocity and acceleration.

$$\text{v}=v{\text{e}}_t=\rho \dot{\beta }{\text{e}}_t$$ $$\text{a}=\frac{d\text{v}}{dt}=v\dot{{\text{e}}_t}+\dot{v}{\text{e}}_t$$

Finding $\dot{{\text{e}}_t}$ isn’t very easy, so instead:

$$\frac{d{\text{e}}_t}{d\beta }={\text{e}}_n$$ $$\dot{{\text{e}}_t}=\dot{\beta }{\text{e}}_n$$ $$v=\rho \dot{\beta }$$

Then:

$$\text{a}=\frac{v^2}{\rho }{\text{e}}_n+\dot{v}{\text{e}}_t$$ $$a_t=\dot{v}=\frac{d}{dt}\Vert {\vec{r}}^{\prime }(t)\Vert$$ $$a_n=\frac{v^2}{\rho }=\kappa \Vert {\vec{r}}^{\prime }(t){\Vert }^2$$

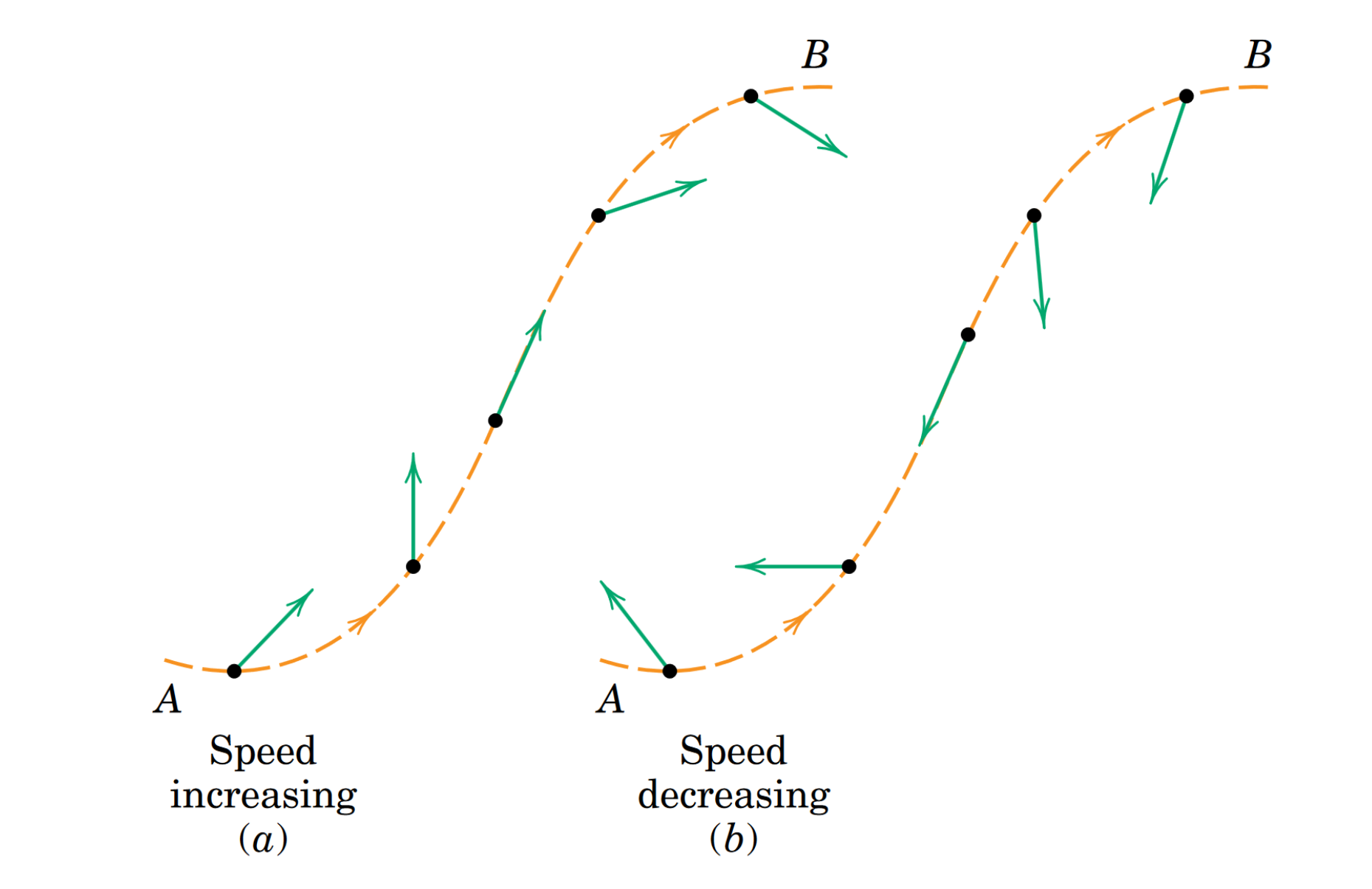
Tangential acceleration changes the magnitude of the velocity.

• $a_t>0$ is being pulled in the direction of the unit tangent vector, speeding up.
• $a_t=0$ means being pulled in no direction with no change in speed.
• $a_t<0$ means being pulled against the direction of the unit tangent, slowing down.

Normal acceleration changes the direction of the velocity.

• $a_n>0$ is pulled in the direction of the normal unit vector. Opposite is vice versa.
• $a_n=0$ has no change in direction.