Heap

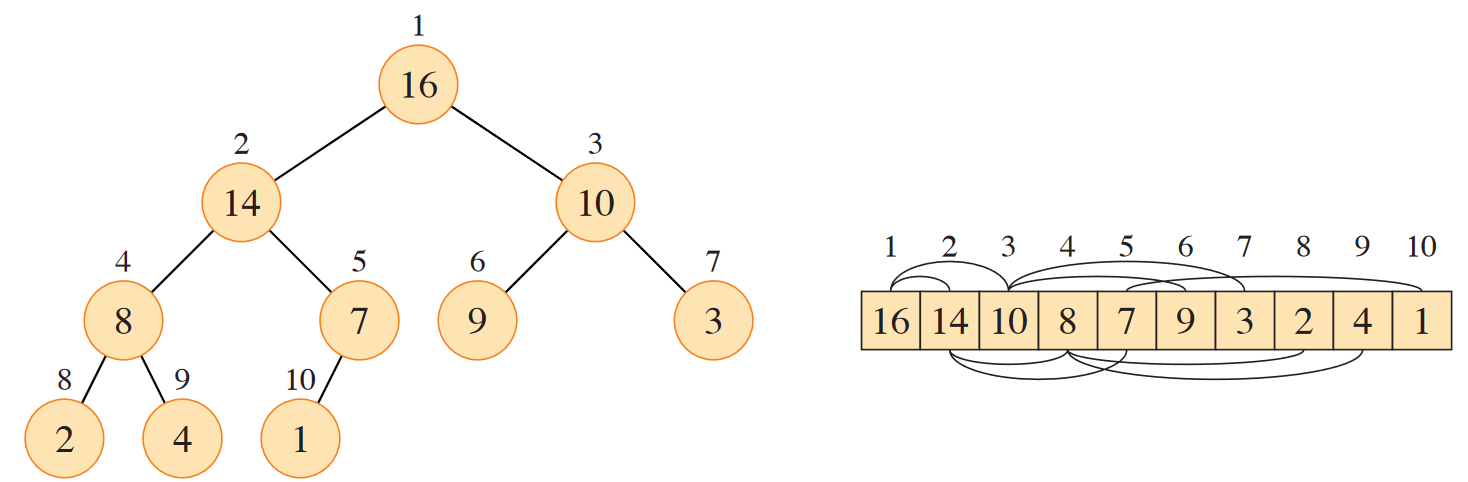
Heaps are a type of data structure, defined as an array $A$ of elements such that it functions according to a heap shape property, such that the heap is an almost complete binary tree (where the last row isn’t full), and the heap order property, which is a specific criterion the heap may fulfil to be valid.

Two common types of heaps are min-heaps and max-heaps, which have the property $A[\text{Parent}(i)]\le A[i]$ and $A[\text{Parent}(i)]\ge A[i]$, respectively.

For a max heap, the maximum element is at the root.

The heap shape property allows us to index:

• $\text{parent}(i)=\lfloor \frac{i}{2}\rfloor$
• $\text{left}(i)=2i$
• $\text{right}(i)=2i+1$

The height of a node in a heap is the number of edges on the longest simple downwards path from the node to a leaf. The height of the heap is the height of its root. Because we talk about a binary heap, its height is $\Theta (\log n)$.

Operations

There are a few operations we want to implement for a max heap:

• Inserting a new element.
• Getting the maximum element.
• Maintaining the max heap property (which runs in $O(\log n)$).

The heapify function enforces the heap order property if it’s violated, with runtime $O(\log n)$. The max heapify function effectively pushes down smaller nodes.

def max_heapify(A, i): # assume i do boundary checking
	l = left(i)
	r = right(i)
	if (A[l] > A[i]):
		largest = l
	else: largest = i
 
	if (A[r] > A[largest]):
		largest = r
	if (largest != i)
		swap(A[i], A[largest]) # max(A[2i], A[2i + 1])
		max_heapify(A, largest)
		# recurse downwards
		# until property is not violated or we've hit a leaf node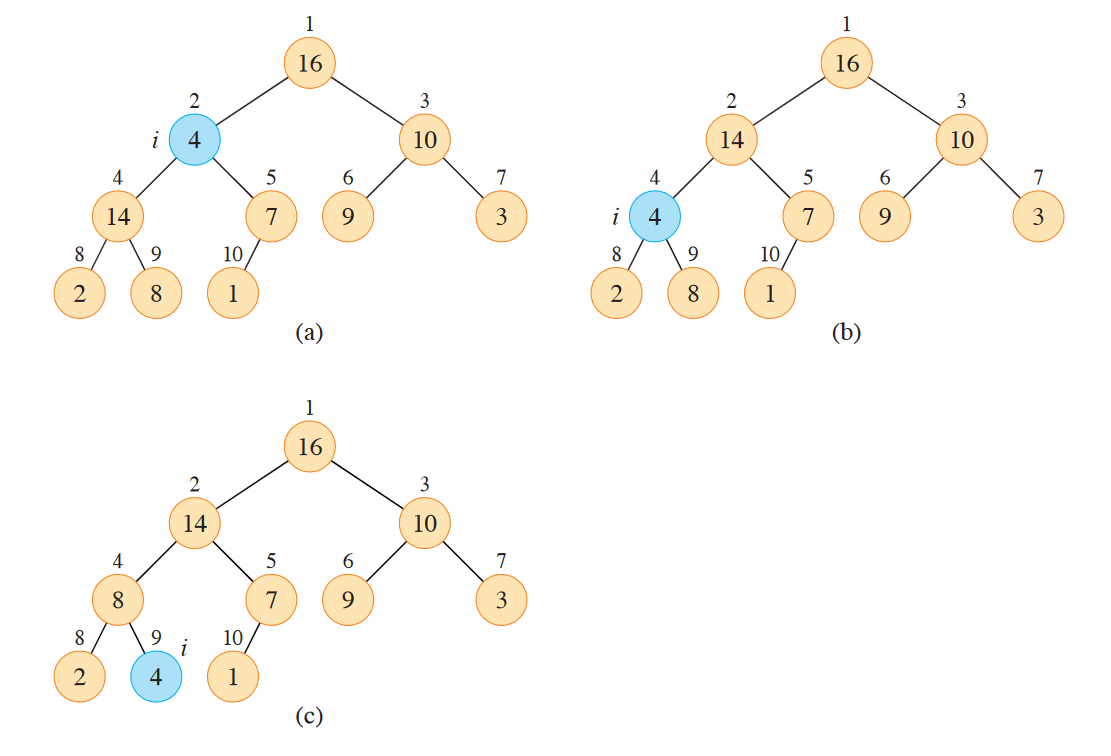

The build-max-heap function constructs a max heap. It starts at the halfway point in the array $A$ because all elements to the right of floor(n / 2) are leaf nodes. Then, we work our way up the heap.

function Build-Max-Heap(A, n):
	for each i = floor(n / 2) -> 1 do
		Max-Heapify(A, i)

Its time complexity is naively $O(n\log n)$, which is a correct upper bound, but not asymptotically tight. However, we can construct a tighter bound:

• At height $h$, there are at most $\lceil \frac{n}{2^{h+1}}\rceil$ nodes. Since we work our way up, the number of nodes at each level decreases exponentially (half the nodes of the previous iteration’s level).
  • This means the number of nodes that require a heapify decreases as we move up the tree. i.e., at the bottom, we do $n/2$ calls to max-heapify, then $n/4$, then $n/8$.
  • Basically, the premise that max-heapify requires $O(\log n)$ is incorrect. It will never swap all the way down to the leaves (at each subtree, it only requires at most one swap).
• The height of the heap is $\lfloor \log (n)\rfloor$.
• Then the runtime is the following. The sum converges absolutely.

$$\sum _{h=0}^{\lfloor \log n\rfloor }\lceil \frac{n}{2^{h+1}}\rceil O(h)\le cn\sum _{h=0}^{\infty }\frac{h}{2^{h+1}}=O(n)$$

Heapsort also relies on heap properties.

See also

• Heap memory, a different construct in programming languages for dynamically allocated, often garbage collected memory
• Priority queue, an abstract data type typically implemented with a heap