Hash collision

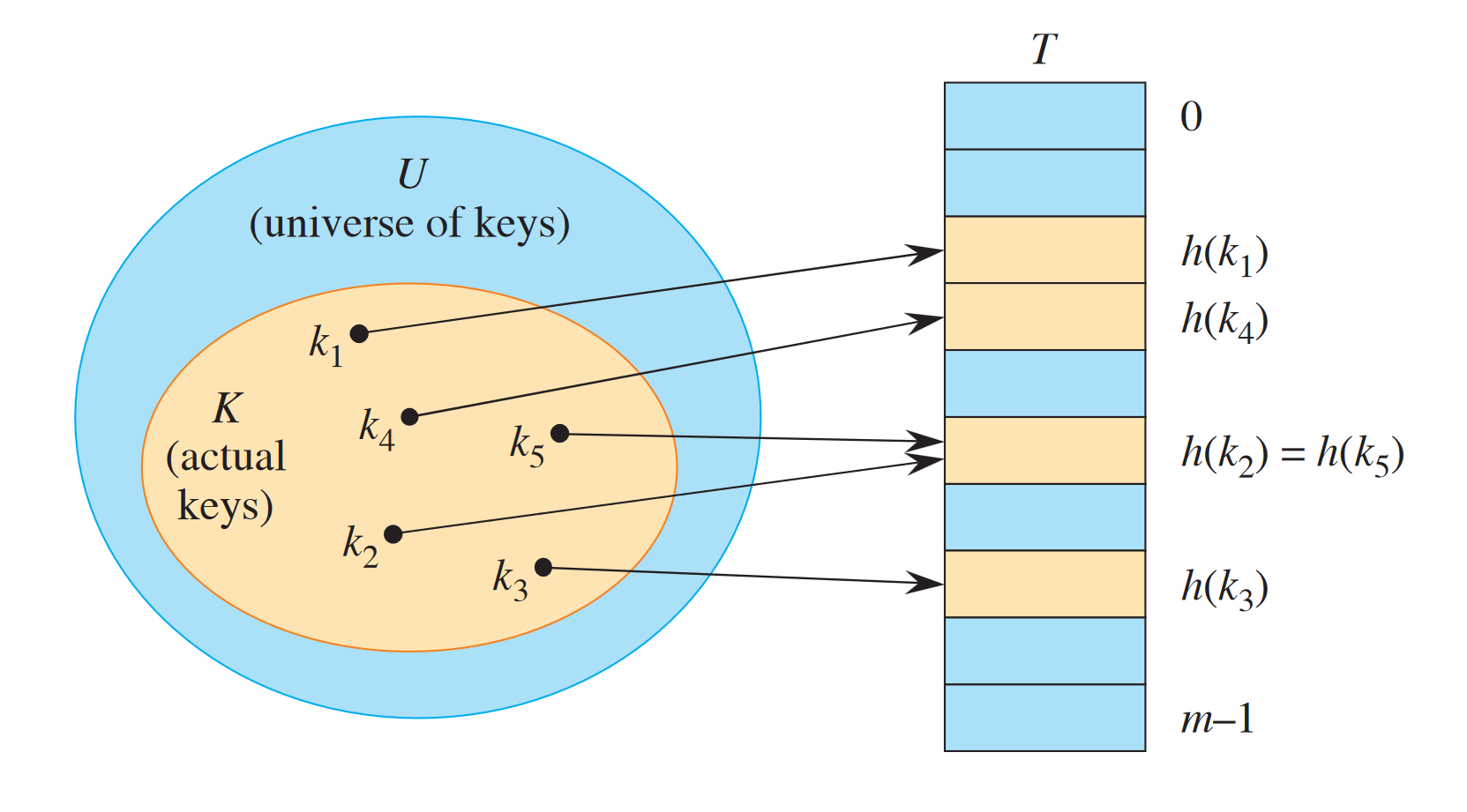
A hash collision occurs when a hash function $h(k)$ maps more than one distinct key to the same value in a hash table of size $m$ — this is one of the fundamental problems with hash tables. We have a few mitigation strategies: open and closed hashing.

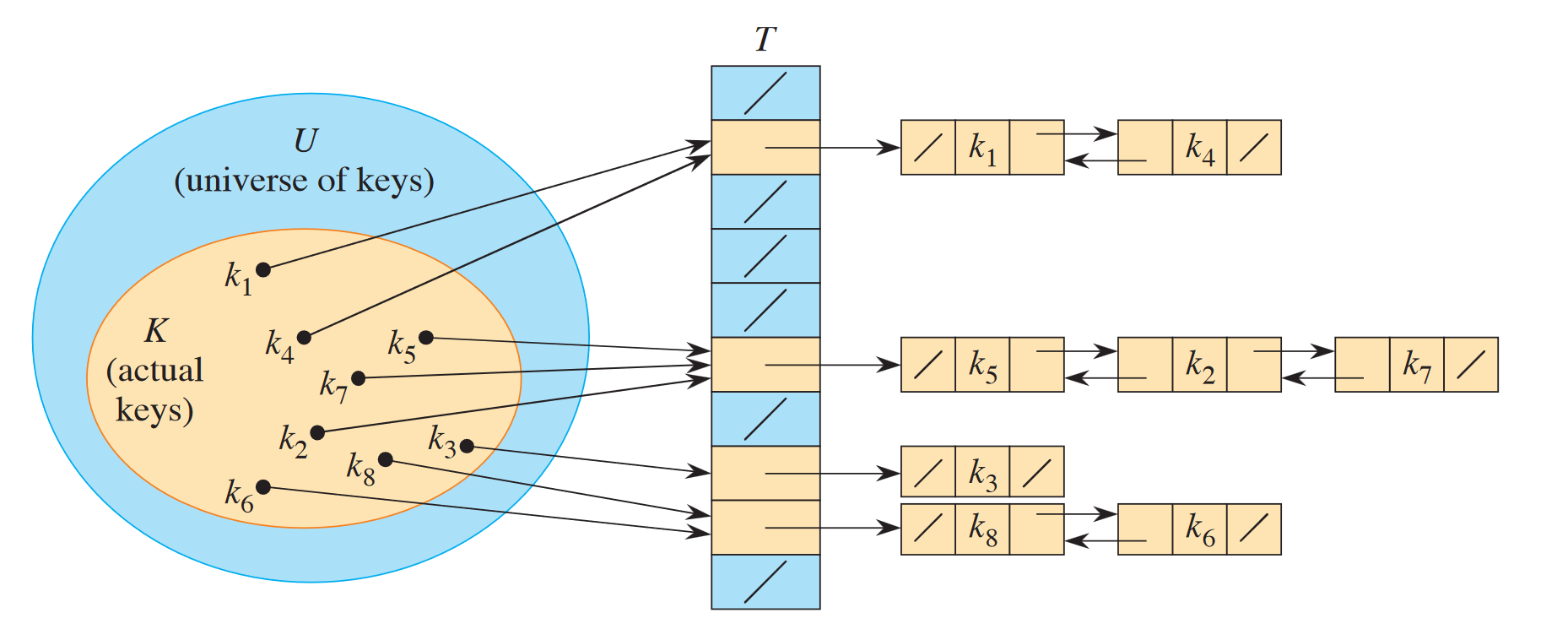
Open hashing

Open hashing (also hashing with chaining) is the idea that we can have array values actually be pointers to linked lists with keys that map to the same entry.

The worst-case time complexity is $O(n)$, but with an ideal hash function $h(k)$, the average list length is 1 and so the average complexity is $\mathcal{O}(1)$.

How do we get there though? So that the average list length is 1?

• We can make the hash table bigger
• Use better hashing functions
  • Making table a prime number
  • Or having the hash function multiply $k$ by a large prime number before taking the modulus
    • i.e., $h(k)=(k\cdot 31)\text{mod}m$

Closed hashing

The idea with closed hashing (also open addressing) approaches is that no two keys will be saved to the same value.

• Linear probing proposes we do: $(h(k)+i)\text{mod}m$ if there’s a collision at $h(k)$.
  • Could lead to clustering, where inserted keys tend to group together. This increases the average search time.
  • In theory, deletion seems complicated. We use a “tombstone” to mark a deleted entry. So that items further down the probe still get searched when needed.
• Quadratic probing proposes a similar idea: $(h(k)+i^2)\text{mod}m$ if there’s a collision.
• Double hashing proposes: $(h_1(k)+i{h}_2(k))\text{mod}m$. This is a good mitigation strategy for clustering with linear probing. It effectively passes the key through two different hash functions.