Game solver

Games are an important application of artificial intelligence programs. Some key implications:

• The state spaces can be very large (the search tree for chess has ~$10^{154}$ nodes).
• Decisions must be made in real-time.
• And it’s easy to determine when a program is doing well!

Definitions

The properties of the games themselves will determine how we design our agent:

• Number of players, i.e., single-player (our opponent is the game), or multi-player games (our opponents may be adversarial or cooperative).
• Randomness. Some games are deterministic (no random elements, change in state is controlled by the players), and some are stochastic (where the change in state is partially determined by chance, like poker).
• Information available. Some games have perfect information (where we can fully observe the game state, like chess). Some are imperfect (part of the state is hidden, like Scrabble).
• Constant sum games (like rock-paper-scissors) have the total payoff to all players constant, where you win what the other players lose. In a non-zero sum game (like the prisoner’s dilemma), the total payoff depends on different scenarios.

We define a two-player zero-sum game as consisting of the following components:

• Two players max and min.
• A set of positions $P$ (states of the game).
• A starting position $s\in P$ (where game begins).
• A set of terminal positions $T\subset P$ (where game ends).
• A set of actions E_\max between some positions, representing max’s moves.
• A set of actions E_\min between some positions, representing min’s moves.
• A utility function $U:T\to R$ representing how good each terminal state is for max.
  • We don’t need a utility function for min because we work with a zero-sum game. Whatever max gets is the negative of min’s payoff.

Game trees

A game tree consists of layers for alternating moves between max and min. The root layer is usually associated with max. Leaves are terminal game states labelled with the rewards for max (i.e., utility values; -1 for a loss, 0 for a tie, +1 for a win). Each path from the root to a leaf node represents a potential playthrough of the game.

The goal of the search is to find a path that maximises max’s payoff or equivalently minimises min’s payoff. 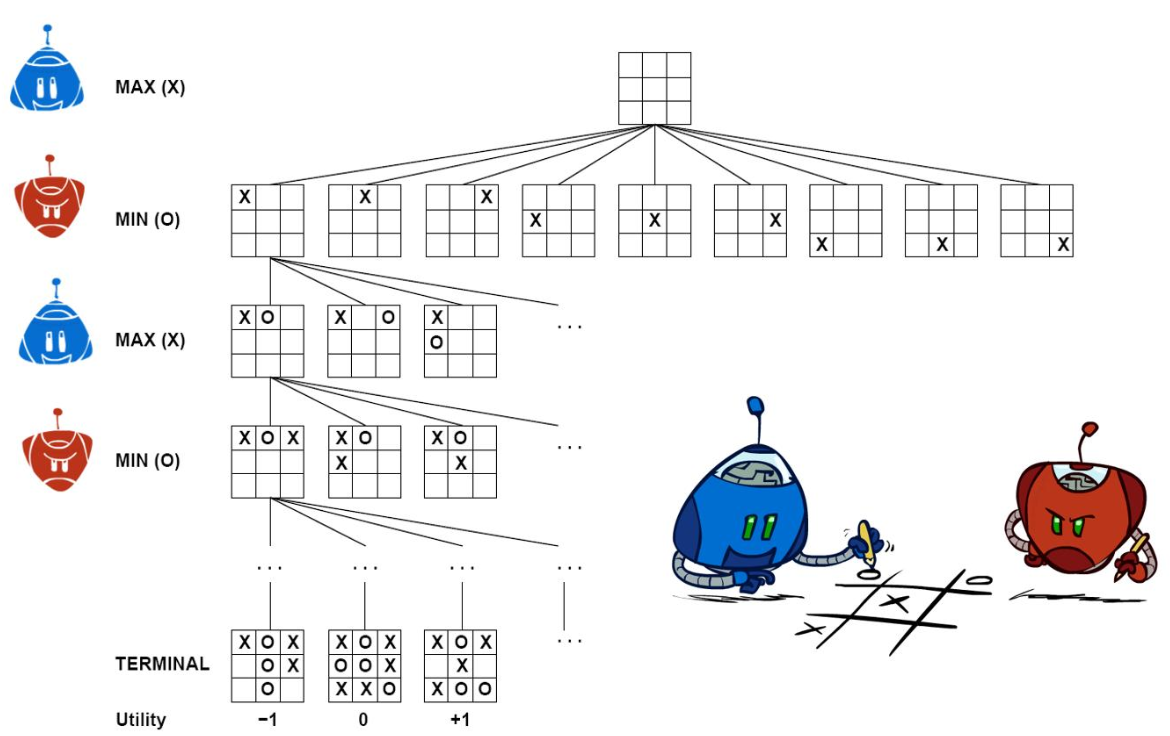In a standard search, a solution is a sequence of moves leading to a goal state. In a game, the strategy for max specifies:

• A move for the initial state.
• A move for all possible states arising from min’s response.
• All possible responses to all of min’s responses to max’s previous moves.

i.e., it specifies what move to make at every contingency. We want algorithms that calculate a strategy (or policy) that recommends a move from each state. Minimax is a strategy that assumes each player makes the optimal choice during their turn.