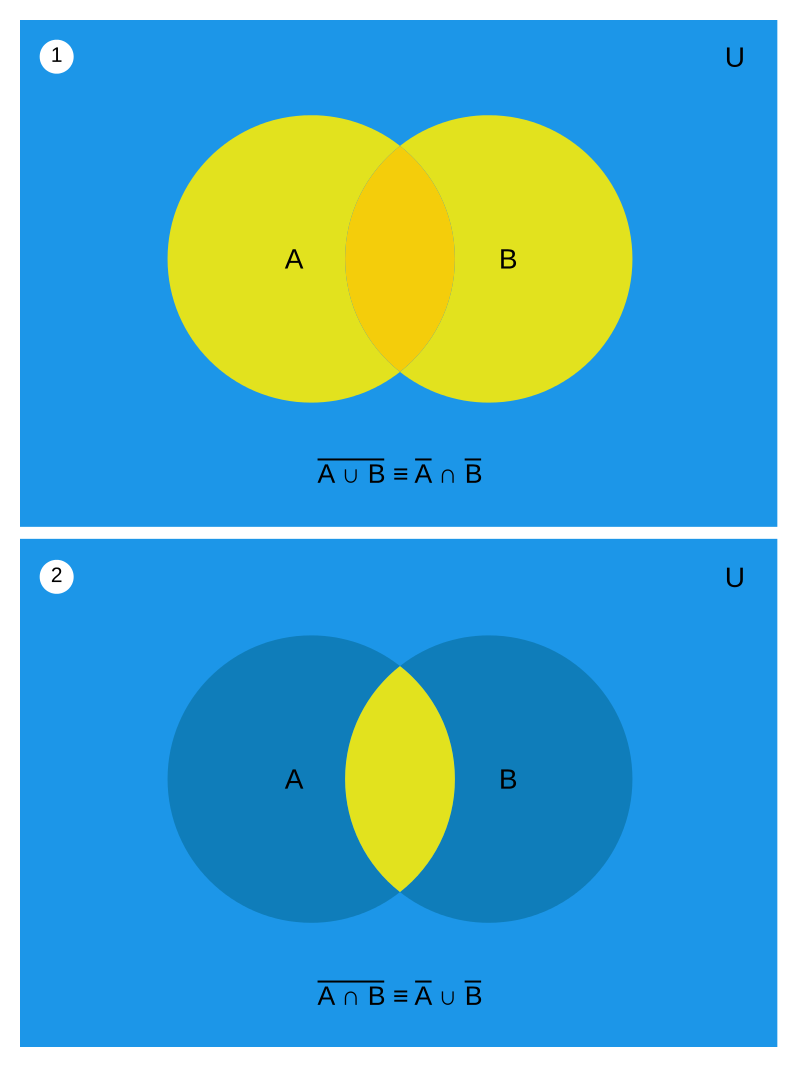
De Morgan's laws

De Morgan’s law is a proposition used in set theory and Boolean algebra. We have a few different equivalent representations that we might see. This is used in programming and hardware design to simplify complicated conditional statements or logic functions.

In Boolean algebra form:

$$\overline{A+B}=\bar{A}\bar{B}$$ $$\overline{AB}=\bar{A}+\bar{B}$$

Helpfully, by De Morgan’s laws, NAND(A, B) is equivalent to NOT A & NOT B. This lets us re-express many logic circuits in terms of NAND.

In set notation:

$$(A\cup B{)}^{\prime }=A^{\prime }\cap B^{\prime }$$ $$(A\cap B{)}^{\prime }=A^{\prime }\cup B^{\prime }$$

This generalises for more sets. Let $T$ be a set, and $\mathcal{S}$ be a collection of subsets of $T$. If ${\cap }_{S\in \mathcal{S}}S$ denotes all intersections of the subsets $T$ and of a set $S$, then we say:

$$T\backslash ({\cup }_{S\in \mathcal{S}}S)={\cap }_{S\in \mathcal{S}}(T\backslash S)$$ $$T\backslash ({\cap }_{S\in \mathcal{S}}S)={\cup }_{S\in \mathcal{S}}(T\backslash S)$$