Variational autoencoder

In deep learning, variational autoencoders (VAEs) are a type of generative network based on autoencoders with the key differences:

• They’re probabilistic instead of deterministic, so their outputs are partially determined by chance, even after they’ve been trained.
• They’re generative, so they can generate new instances that look like they were sampled from the training set. This is done by imposing a distribution constraint on the latent space so that each class doesn’t necessarily occupy a distinct subspace.

Instead of occupying a fixed embedding, the encoder generates a normal distribution (with mean $\mu$ and standard deviation $\sigma$). An embedding is instead sampled from the distribution and the decoder decodes the sample to reconstruct the input. 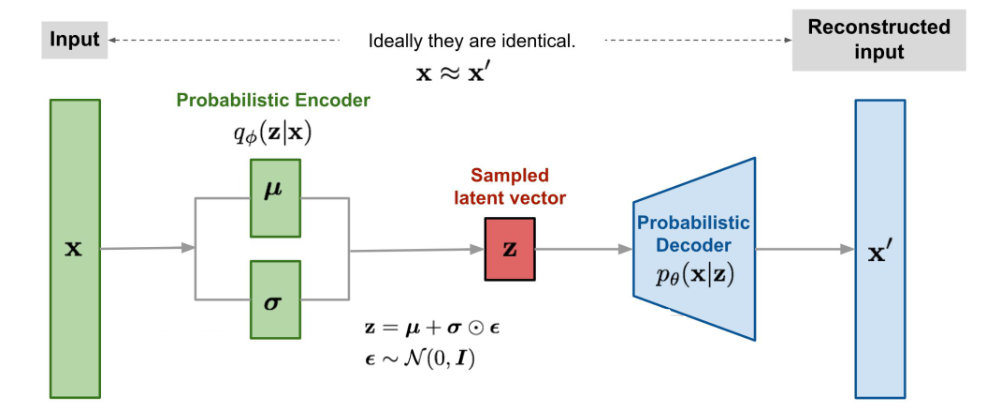One key idea is that we want the encoder distribution $q_{\phi }$ to be close to prior $p(z)=\mathcal{N}(0,I)$. One metric we could use to measure the difference (i.e., the loss function) between two distributions is the KL divergence. Autoencoders have a problem for generating complicated data, i.e., images. They tend to generate blurry images with blurry backgrounds, since they minimise the MSE loss by predicting the average pixel.

In code

VAEs are, in practice, slightly different from regular autoencoders in their implementations. This time, we don’t define a nn.Sequential() block for the encoder/decoder. We define each layer separately.

We add a special re-parameterisation function used to sample from the probability distribution. This allows us to use backprop through a stochastic variable.

def reparameterize(self, mu, logvar):  
    if self.training:  
        std = logvar.mul(0.5).exp_()  
        eps = std.data.new(std.size()).normal_()  
        return eps.mul(std).add_(mu)  
    else:  
        return mu
 
def forward(self, x):  
    mu, logvar = self.encode(x.view(-1, 28 * 28))  
    z = self.reparameterize(mu, logvar)  
    return self.decode(z), mu, logvar

In this case, the encoder returns the mean and log variance of the latent distribution. This is passed into the reparameterize() function, which samples using mu and logvar.

The reparameterize function calculates the standard deviation, then generates a tensor eps with the same size as std, sampled from a unit Gaussian distribution with $\mu =0$, ${\sigma }^2=1$. Then, it returns a re-parameterised sample from a Gaussian distribution with mean mu and standard deviation std.

The VAE also has two modes of operation. One is training mode, where it applies the reparameterize() function (to facilitate backprop). The other is inference mode, which ignores any stochasticity.