Trigonometric substitution

Trigonometric substitution is an integration that involves a change of variables. It relies on the Pythagorean theorem as a linear map. Your best friend is something called a reference triangle.

A brief example

Say we want to integrate $\int \frac{1}{\sqrt{4-x^2}}dx$. We may observe, following $a^2+b^2=c^2$, that we can build a triangle that looks like the below. 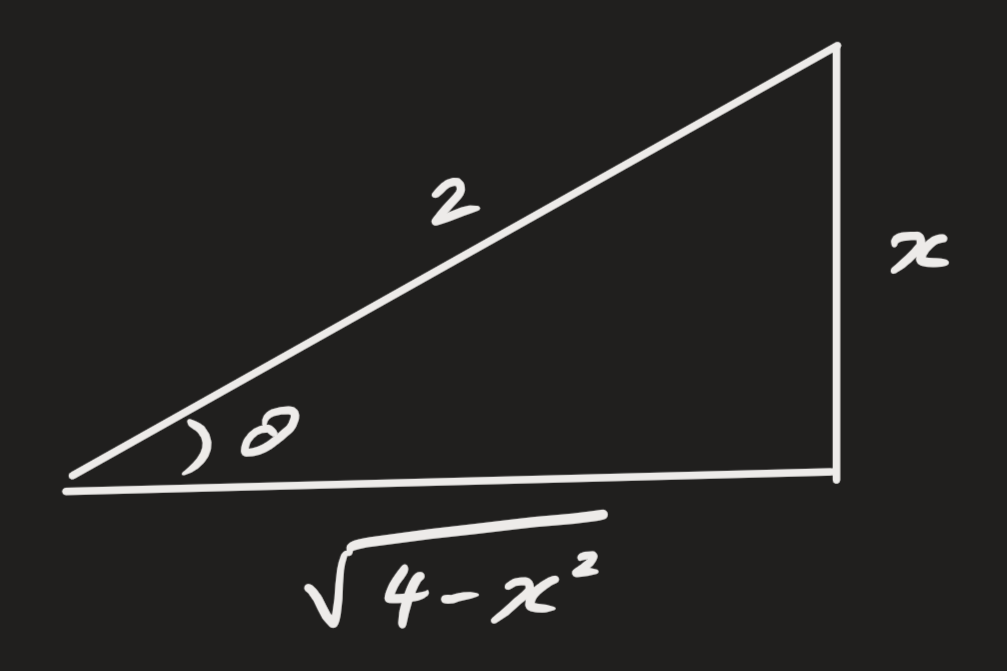So we get: $\sin \theta =\frac{x}{2}$ $\cos \theta =\frac{\sqrt{4-x^2}}{2}$ which we can re-arrange to: $x=2\sin \theta$ $\sqrt{4-x^2}=2\cos \theta$ You can probably guess by substituting we get a simpler integrand: $\int \frac{1}{\sqrt{4-x^2}}dx=\int \frac{2\cos \theta }{2\cos \theta }d\theta =\int 1d\theta =\theta +C$ and then we have to convert back in terms of $x$: $\arcsin \frac{x}{2}+C$ Some considerations:

• There are some rational functions that we can’t decompose with partial fractions, with a quadratic term in the numerator with no real roots — we can complete the square and factor that way