Signed number

Numbers are either signed or unsigned. Unsigned numbers don’t have a positive or negative sign, i.e., they are only positive. In the context of computer systems, unsigned numbers increase the absolute value of numbers we can represent in data. In a $k$-bit system, we can represent individual numbers from 0 to $2^k-1$.

A key question is with how we can represent signed numbers in binary. The most popular approach involves two’s complement, where the most significant bit is a sign bit.¹ 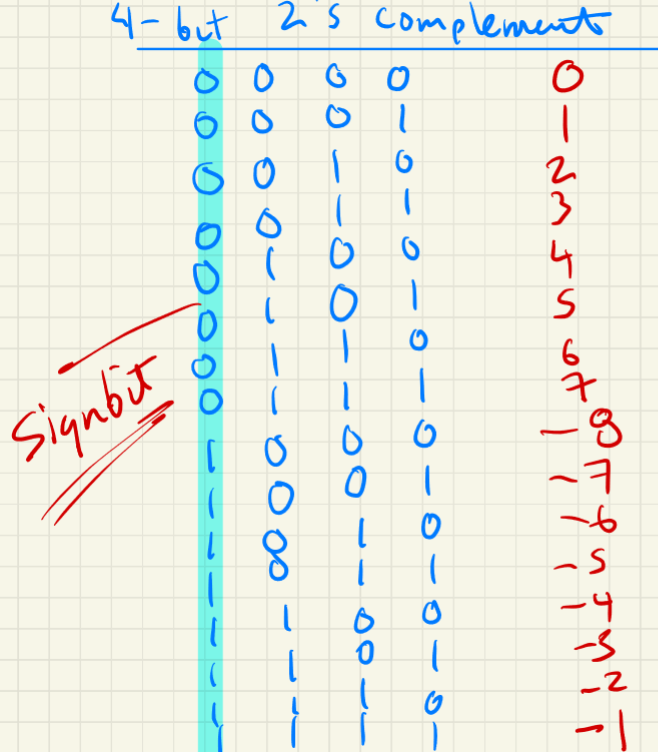Observe how our number representation here still lines up with reality. If we add a positive and a negative number together, we get the correct result! Really cool. We can represent numbers in a $k$-bit system in the interval: $[-2^{k-1}:2^{k-1}-1]$.

And how do we find the negative equivalent of a number? We can flip all the individual bits and add 1:

$$010001=(17{)}_{10}$$ $$101110+1=101111=(-17{)}_{10}$$

Sign extension

What about a sign extension, like what we get when we type cast? When we convert from an int (32-bits) to a long (64-bits), we do a sign extension and replicate the most significant bits. Here’s an example for a 6-bit to 8-bit conversion:

$$101111=(-17{)}_{10}$$ $$11101111=(-17{)}_{10}$$

We can still do our equivalence check from above to verify this holds.

In hardware, sign extension is done by branching off the most significant bit into more wires. For example:

Footnotes

1. From Prof Anderson’s lecture notes. ↩