Principal value integral

The principal value integral (also the Cauchy principal value) allows us to compute improper integrals that would otherwise diverge.

$$\text{PV}{\int }_{-\infty }^{\infty }f(x)dx=\underset{R\to \infty }{\lim }{\int }_{-R}^{R}f(x)dx$$

Part of the set-up is in understanding whether we’re dealing with an even or odd function. For an even function:

$${\int }_0^{\infty }f(x)dx=\frac{1}{2}{\int }_{-\infty }^{\infty }f(x)dx$$

which enables us to use the principal value.

$${\int }_{-\infty }^{\infty }f(x)dx={\oint }_{C_R}f(z)dz=2\pi i\sum _{k=1}^n\text{Res}(f(z);z_k)$$

Use of complex analysis

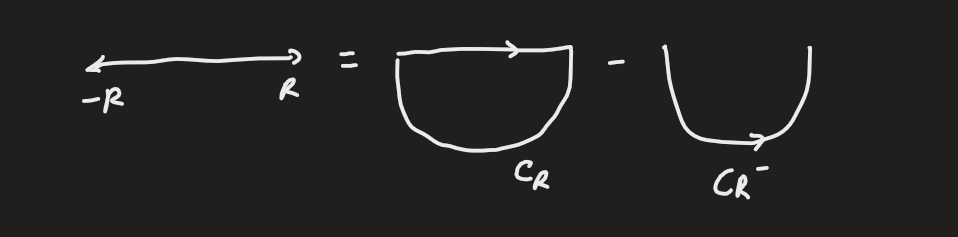
This is important because the idea is that we integrate over a line on the real axis in $[-R,R]$. If we then close the contour by adding a semi-circle that encloses all of the poles of $f$. Let $C_R$ be the simple closed contour and $C_R^{+}$ be the upper semi-circle excluding the line on the real axis, i.e., $C_R$ is the union of $C_R^{+}$ and $[-R,R]$.

$${\oint }_{C_R}f(z)dz={\int }_{C_R^{+}}f(z)dz+{\int }_{-R}^{R}f(x)dx=2\pi i\sum _{k=1}^n\text{Res}(f(z);z_k)$$

by Cauchy’s residue theorem. Then we re-arrange:

$${\int }_{-R}^{R}f(x)dx={\oint }_{C_R}f(z)dz-{\int }_{C_R^{+}}f(z)dz$$

This assumes we have finitely many singular points in $C_R$. Conveniently the subtracted term often is equal to 0, by the theorems given in Jordan’s lemma.

DO NOT TURN OFF YOUR BRAIN HERE. THE PROBLEM COMES WHEN FINDING A CONTOUR WHERE JORDAN’S LEMMA IS TRUE.¹

A nice reality check is that our final result should be positive. When we take $C_R^{-}$, we actually work clockwise (think about it for a second) instead of counter-clockwise. So instead of subtracting with the negative semi-circle, we actually add. Intuitively, look at the exponential in the integral. Think about where it ends up being small (i.e., approaching 0), and we take that.

Why does it matter, if by Jordan's lemma, the term reduces to 0 anyways?

We get our residues from the choice of curve. If we choose this wrong and just write “by Jordan’s lemma”, we are fundamentally misunderstanding the problem, and we might get wrong residue values.

Another trap: when we take the negative curve, our overall curve ends up being clockwise. The residue theorem applies for counter-clockwise contours, not for clockwise contours. So instead of taking the positive algebraic sum of the residues, we actually take the negative algebraic sum.

$$\underset{R\to \infty }{\lim }{\int }_{-R}^{R}f(z)dz=-\sum _{k=1}^n\text{Res}(f(z);z_k)+{\int }_{C_R^{-}}f(z)dz$$

Another trap: what if our function looks like:

$$f(z)=\frac{\cos x}{(x^2+4{)}^2}$$ $$\cos x=\frac{e^{iz}+e^{-iz}}{2}$$

Because one of the terms will always blow up to infinity, we can’t just use either top or bottom semi-circle and cancel it out by Jordan’s lemma. Doing so is again misunderstanding the problem. Instead what we do is:

$$e^{ix}=\cos x+i\sin x$$ $$\text{Re}\left(PV{\int }_{-\infty }^{\infty }\frac{e^{ix}}{(x^2+4{)}^2}dx\right)$$

where we use the upper semi-circle.

If our function has strictly real poles, then we use indentation of contours.

Thinking about improper integrals

Recall when we think about improper integrals, we should split the function at points. We can’t just evaluate it like above. But by introducing the principal value we can.

A proposition: if ${\int }_{-\infty }^{\infty }f(x)dx$ converges in the improper integral sense, then:

$${\int }_{-\infty }^{\infty }f(x)dx=PV{\int }_{-\infty }^{\infty }f(x)dx=\underset{R\to \infty }{\lim }{\int }_{-R}^{R}f(x)dx$$

i.e., if an integral converges, then the principal value is the same as the integral. If it diverges, it still may have a principal value.

Footnotes

1. ”Total misunderstanding. Acting like a robot.” - Prof Nachman ↩