Indentation of contours

In complex analysis, indentation of contours is an approach we use if a rational complex function $f(z)=\frac{p(z)}{q(z)}$ has strictly real poles (i.e., they’re on the real axis). This is an extension of the discussion of principal value integrals.

By theorem, suppose $f(z)$ has a simple pole at $z_0\in \mathbb{R}$. Let $C_R^{+}$ be the semi-circle $z_0+r{e}^{i\theta }$ ($\theta \in [0,\pi ]$) traversed counter-clockwise. Then:

$$\underset{r\to 0}{\lim }{\int }_{C_r}f(z)dz=\pi i\text{Res}(f(z);c)$$

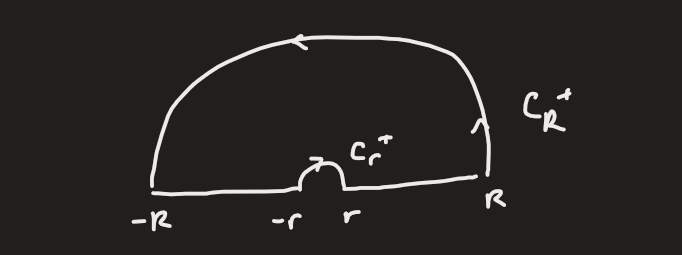Note that for the “indent”, it actually briefly goes clockwise.

$${\oint }_{C_{R}r}f(z)dz-{\int }_{C_r^{+}}f(z)dz-{\int }_{C_R^{+}}f(z)dz={\int }_{-R}^{r}f(x)dx+{\int }_r^{R}f(x)dx$$

We know by Jordan’s lemma that:

$$\underset{R\to \infty }{\lim }{\int }_{C_R^{+}}\frac{e^{iz}}{z(1+z^2)}dz=0$$

So:

$$-{\int }_{C_R^{+}}f(z)dz=0$$