Prefix tree

A prefix tree (also trie, digital tree) is a search tree where the data are strings, and the edges are defined by individual characters. This supports fast pattern matching for information retrieval.

We define a standard trie for a set of $s$ strings from an alphabet $\Sigma$, such that no string in $S$ is a prefix of another string, as an ordered tree $T$ with the following properties:

• Each node of $T$, except the root node, is labelled with a character of $\Sigma$.
• The ordering of the children of an internal node of $T$ is determined by a canonical ordering of the alphabet $\Sigma$.
• $T$ has $s$ external nodes (i.e., at the bottom of the tree), each associated with a string of $S$, such that the concatenation of the node labels on the path from the root to an external node $v$ of $T$ yields the string of $S$ associated with 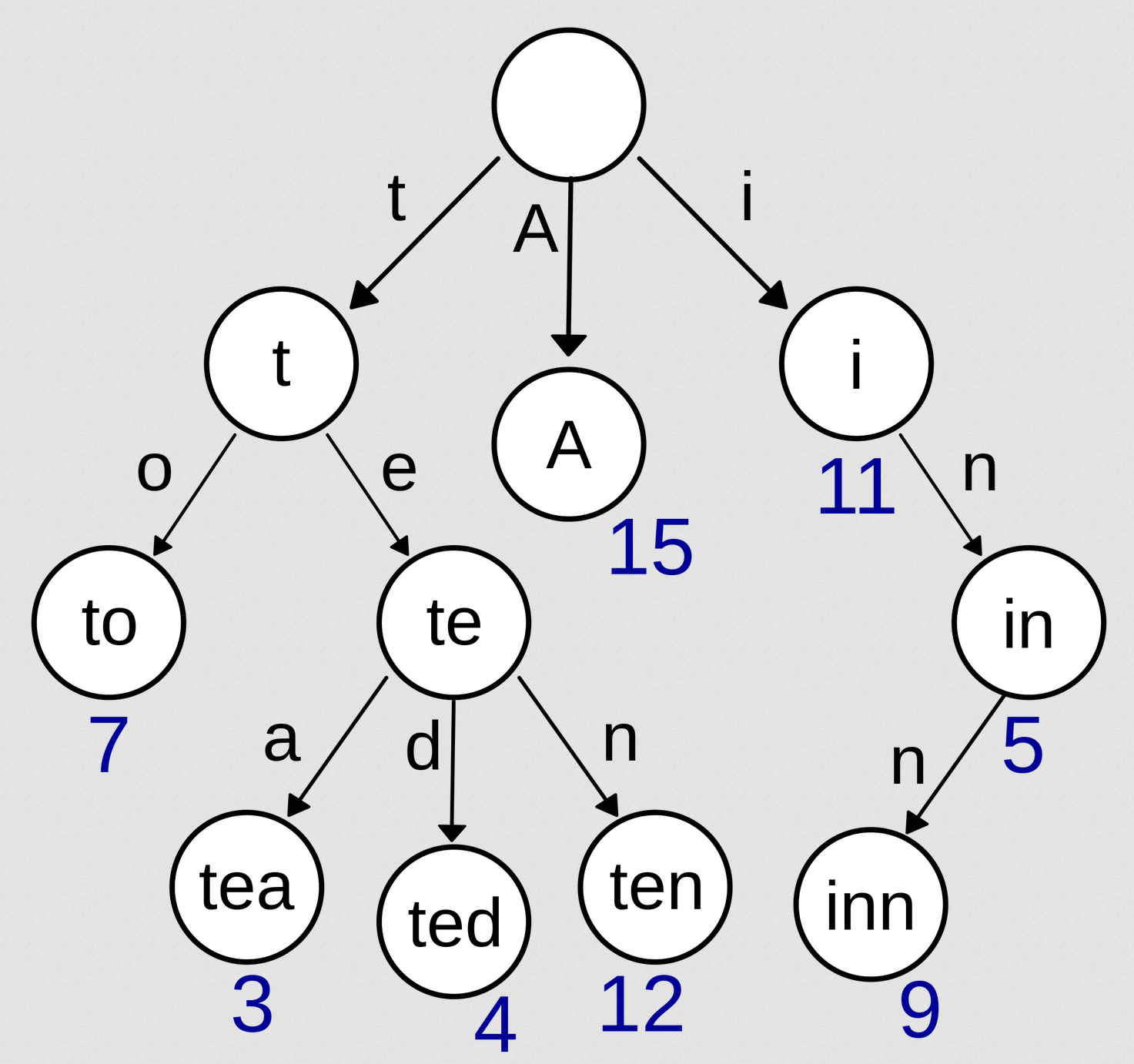$v$. It’s easy to see that the time complexity for a string search of size $m$ in an alphabet of size $d$ will be $O(m\cdot f(d))$, where $f$ is the look-up time complexity. Depending on the alphabet, this could be linear time (linked list), logarithmic time (tree set), or constant time (hash map/set, vector).

Then, the time complexity for insertion is $O(md)$.

Variation

Since standard tries potentially have many children with one node, this is an inefficient use of space. A compressed trie enforces that each internal node has at least two children, otherwise it holds the entire substring.

We say that a node $v$ of $T$ is redundant if $v$ has one child and is not the root. We also say that a chain of $k\ge 2$ edges $(v_0,v_1)(v_1,v_2)\cdots (v_{k-1},v_k)$ is redundant if $v_i$ is redundant for $i\in [1,k)$ and $v_0$ and $v_k$ aren’t redundant.