Mutual inductance

Mutual inductance is the resulting phenomenon when two inductive coils are placed close together, explained by Faraday’s law, Lenz’s law, and Ampere’s law. The changing current of one coil will induce a voltage in the other.

Since we discuss linear circuits, we can apply superposition such that the total voltage is the sum of voltages from the self-inductance of the wire and the mutual inductance of the other coil.

$$v_1=L_1\frac{d{i}_1}{dt}\pm M\frac{d{i}_2}{dt}$$ $$v_2=L_2\frac{d{i}_2}{dt}\pm M\frac{d{i}_1}{dt}$$

Observe the plus/minus. If the flux of both are opposite where the coils meet, we’re operating in subtractive mode. Otherwise we operate in the additive mode.

Dot convention

As a result of the above, we denote an easy way to figure out if we operate in additive or subtractive mode, using dots. 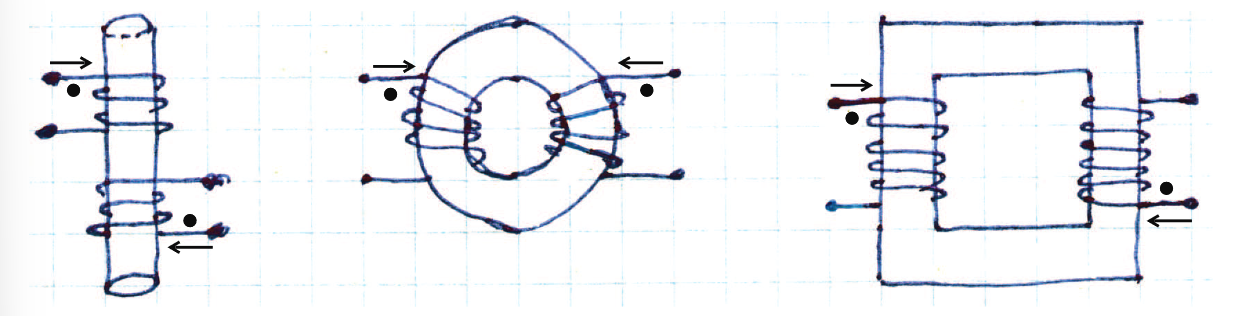We are in additive mode if the current reference directions are either both into or both out of these terminals (the ref. directions are up to us to decide, as long as we’re being consistent).

Multiple coupled inductors

So far we’ve discussed two inductors. When we extend this to more inductors, we get a pretty comparable set of equations:

$$\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right]=\left[\begin{array}{ccc}{L}_1& \pm M_{12}& \pm M_{13}\\ \pm M_{21}& L_2& \pm M_{23}\\ \pm M_{31}& \pm M_{32}& L_3\end{array}\right]\left[\begin{array}{c}{i}_1^{\prime }\\ i_2^{\prime }\\ i_3^{\prime }\end{array}\right]$$

The square matrix is called the mutual inductance matrix. This is extendible to more inductors.

Electromagnetic foundations

We define the inductance $L_{12}$ as the inductance in a second current loop as the result of one current loop. Under static conditions, this is given by:

$$L_{12}=\frac{{\Lambda }_{12}}{i_1}=\frac{N_2}{i_1}{\iint }_{S_2}{\vec{B}}_1\cdot d\vec{s}$$

Think about this intuitively for a second. The flux is just by the first field through the second surface.