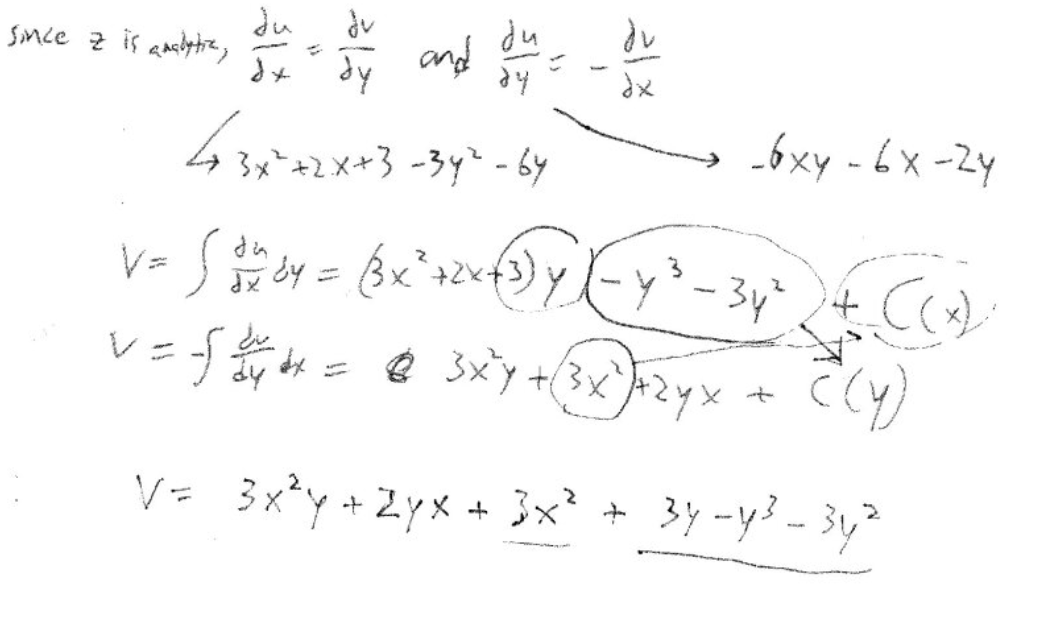Harmonic function

We say that a real-valued function $u(x,y)$ is harmonic if:

$$\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=0\forall (x,y)\in I$$ $${\nabla }^{2}u={\nabla }^{2}v=0$$

where ${\nabla }^2$ is the Laplacian operator.

If a complex function $f=u+iv$ is analytic in a domain $D$, then the functions $u$ and $v$ are harmonic.

If we are given $u$ is harmonic in $D$, then it’s possible to find another function $v$, the harmonic conjugate such that $f$ is analytic in $D$. We need to integrate to find this conjugate (without forgetting the constant):