ReLU

The rectified linear unit (ReLU) is a popular activation function used in modern deep learning. It’s defined by:

$$\text{ReLU}(x)=\max (0,x)$$

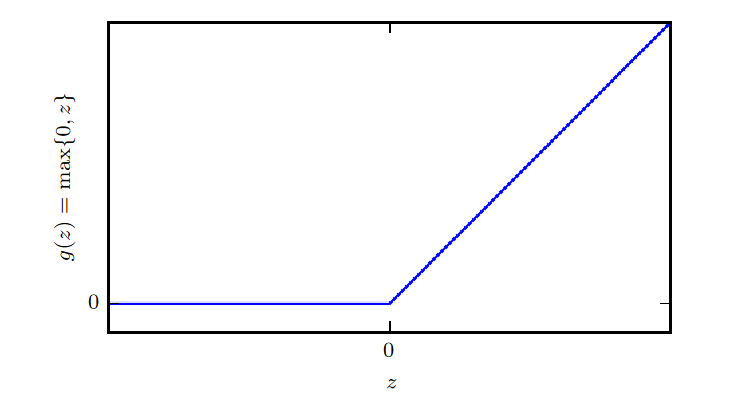We set the derivative of ReLU at $x=0$ as 0, even though it’s discontinuous there. The derivative is functionally the unit step function:

$$\frac{d}{dx}\text{ReLU}(x)=u(x)$$

Motivation

As a rule of thumb, we should always just start with ReLU by default, instead of its variations. ReLU is a powerful activation function because it’s so computationally efficient.

ReLU’s derivatives are well-behaved, because it either vanishes or it lets the input through. This helps mitigate the vanishing gradient problem.

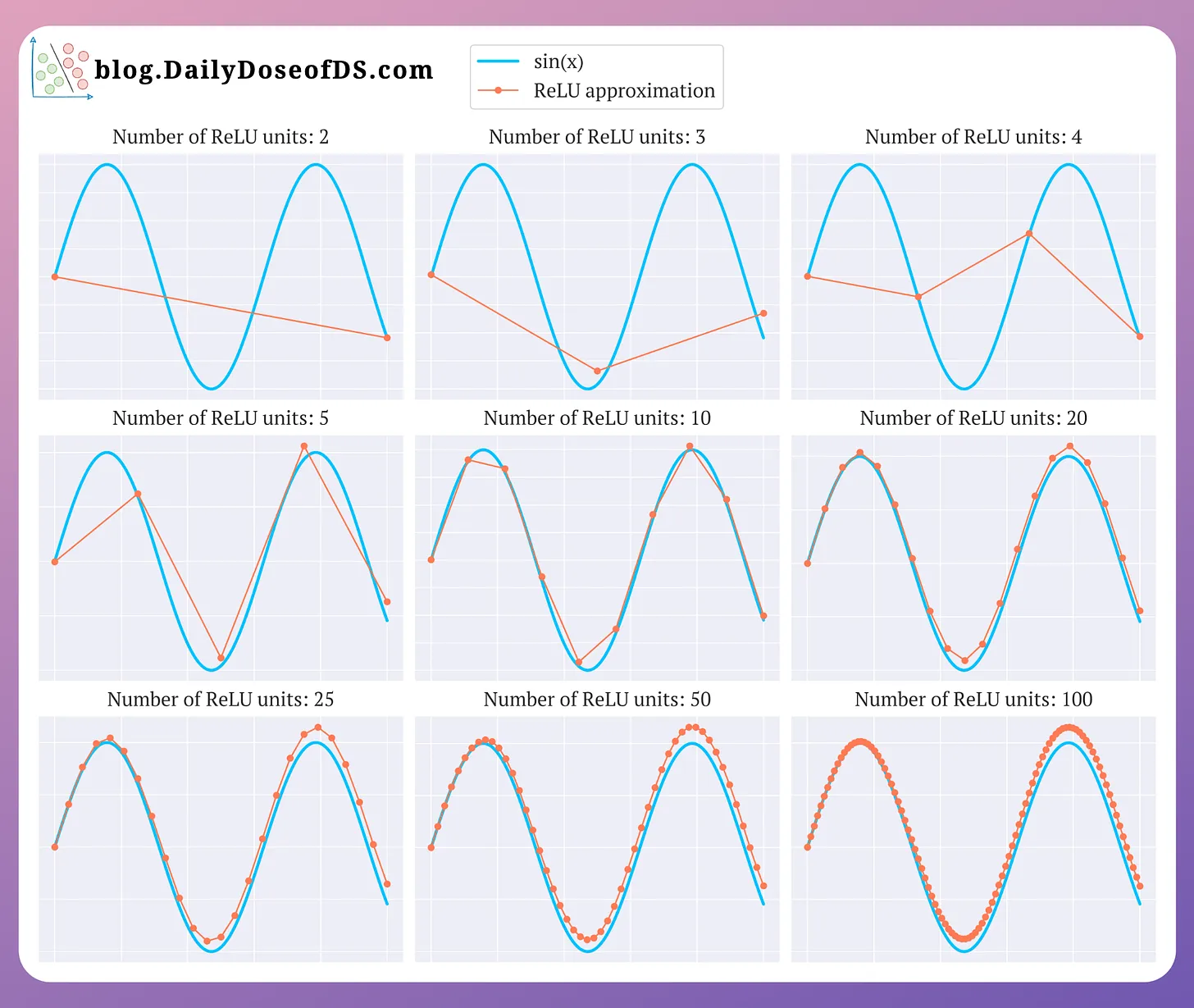
Multiple translated ReLU units offer piecewise linearity that approximates non-linearity. What this means is that with a sufficiently high number of ReLU units, we can approximate any non-linear function:

$$f(x)\approx c+\sum _k{w}_k\ast \text{ReLU}(x-b_k)$$

where $b_k$ are horizontal shifts. Approximating $\sin (x)$:¹

Variations

Since ReLU’s derivative is discontinuous at $x=0$, we’re motivated to explore continuous approximations of ReLU. We can approximate ReLU with continuous functions: SiLU and the softplus function.

The softplus function is defined by:

$$\zeta (x)=\log (1+e^x)$$

It’s useful in producing the $\sigma$ parameter of a normal distribution.

In code

In PyTorch, we have:

y = torch.nn.relu(x)
y = torch.nn.functional.relu(x)

Footnotes

1. From this great article by Avi Chawla at Daily Dose of Data Science. ↩