Maximum flow

The maximum flow problem is a graph problem, where given a flow network and a capacity constraint and flow conservation, we want to find the maximum flow in the network.

The flow network is defined as a directed graph $G=(V,E)$ with the following properties:

• All edges $(u,v)\in E$ have a non-negative capacity $c$.
• $(u,v)\in E⟹(v,u)\notin E$, i.e., if we have an edge from $u$ to $v$, we cannot have a direct edge in the opposite direction between $v$ to $u$.
• $(u,v)\notin E⟹c(u,v)=0$, i.e., if a direct edge doesn’t exist between $(u,v)$, then the capacity of that edge is 0, i.e., it cannot support any flow.
• There are no self-loops.
• $G$ is connected, i.e., $\forall v\in V$, there exists a path from the source to $v$ and from $v$ to the sink.

The flow function $f:V\times V\to \mathbb{R}$ between two vertices $u,v\in V$ has two properties:

• Capacity constraint — the flow cannot be negative and is bounded by the capacity of the edge, i.e., $\forall u,v\in V,0\le f(u,v)\le c(u,v)$,
• Flow conservation — the amount of flow entering a vertex is equal to the flow exiting a vertex.

At any point, all edges in the network essentially have an associated capacity and flow. We also define:

• Residual capacity — what is leftover from the flow. $c_f(u,v)=c(u,v)-f(u,v)$.
• Residual network — the resulting graph where the forward edges are given by $C-f$, and the backwards edges are given by $f$. i.e., we essentially reverse the edges of the flow network, where we add additional edges for the residual capacity. Note then, that $|E_f|\le 2|E|$.
• Augmenting path — a simple path from source to sink in the residual network $G_f$.

Algorithms to solve maximum flow include the following. Both in principle rely on the terms defined above.

• Ford-Fulkerson algorithm
• Edmonds-Karp algorithm

ford fulkerson residual capacity on path: bottleneck of path, minimum residual capacity edge

Problems

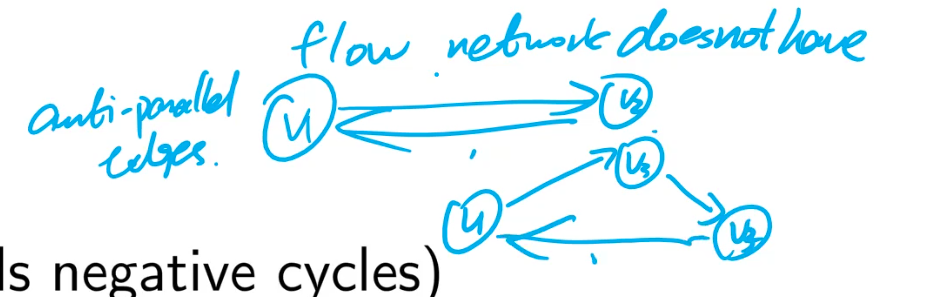
must have no anti-parallel edges flow networks cannot have anti-parallel edges

multiple sources/sinks algos can only deal with single source single sink, so we have a pseudo source/sink

edge disjoint paths no two paths share an edge, multiple paths can go through the same nodes

ignore the last one: find number of independent paths not true or vaguely stated, bc multiple definitions for it

vertex capacity we can’t model it right away like our flow network, so we make a transformation