Directional derivative

In multivariable calculus, the directional derivative measures the rate of change of a function in a particular direction (towards a unit vector $\text{u}$) at a given point. A useful definition is as follows:

$$D_{\text{u}}f(a,b)=⟨f_x(a,b),f_y(a,b)⟩\cdot ⟨u_1,u_2⟩$$

The vector of the partials is called the gradient of $f$. So we can rewrite:

$$D_{\text{u}}f(a,b)=\nabla f(a,b)\cdot \text{u}=|\nabla f(a,b)|\cos \theta$$

A key implication of this is that if the gradient points in the same direction as the unit vector, then the directional derivative is at a maximum value. The opposite holds true.

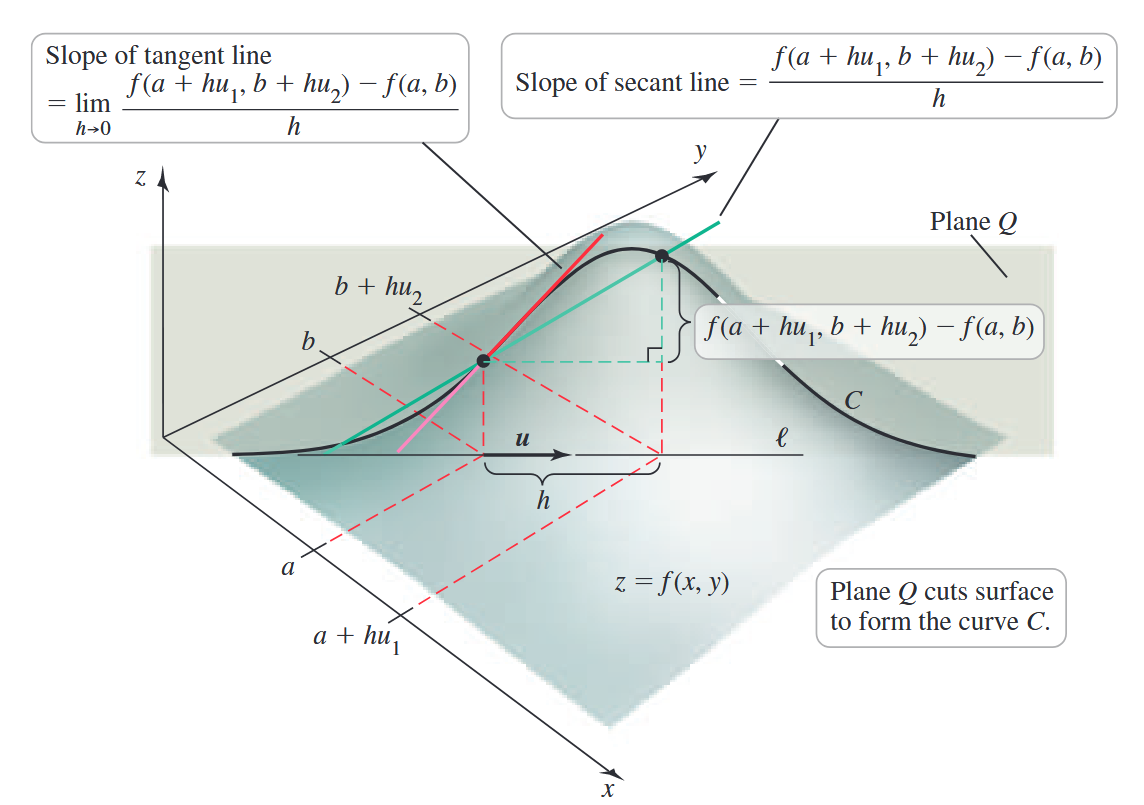
If $f$ is differentiable at $(a,b)$, and $\text{u}=⟨u_1,u_2⟩$ is a unit vector in the $xy$-plane, then we define the directional derivative in the direction of $\text{u}$ as:

$$D_{\text{u}}f(a,b)=\underset{h\to 0}{\lim }\frac{f(a+h{u}_1,b+h{u}_2)-f(a,b)}{h}$$

provided the limit exists.