Chain rule

In single-variable calculus, the chain rule is, for some $y=g(u)$ and $u=f(x)$:

$$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}$$

In multivariable calculus, we extend the idea somewhat. It’s easiest to draw a tree diagram branching out from our main function $z$. We traverse the tree and sum the products of our derivatives: 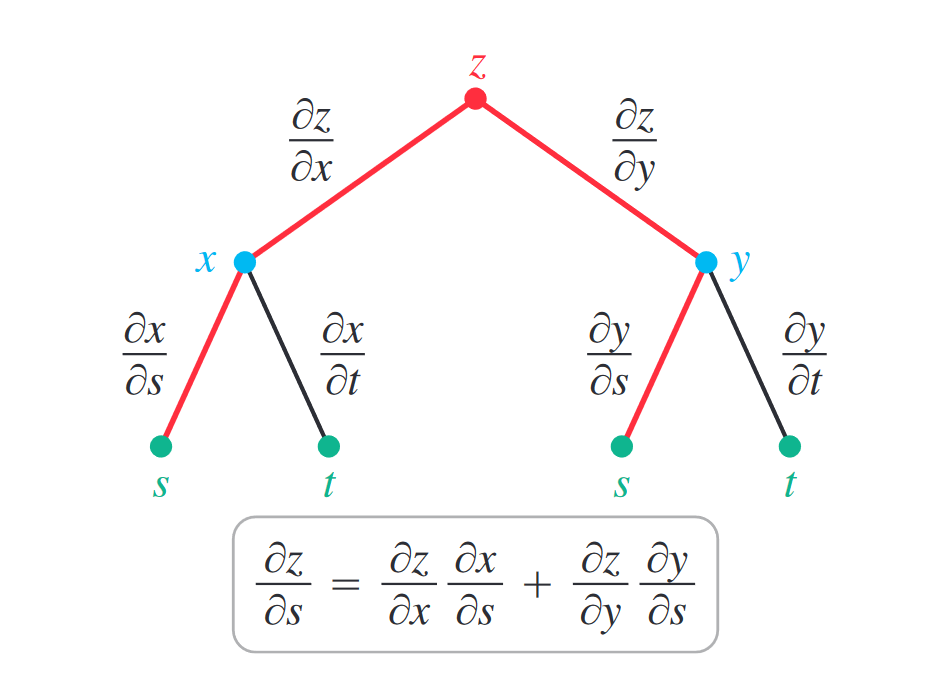Note that for one independent variable, where $z=f(x(t),y(t))$, then we accordingly take full derivatives as followed:

$$\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}$$

We extend the functionality of chain rule with implicit differentiation.

Generalisation

For $\vec{x}\in {\mathbb{R}}^m$, $\vec{y}\in {\mathbb{R}}^n$, and two maps $g:{\mathbb{R}}^m\to {\mathbb{R}}^n$, $f:{\mathbb{R}}^n\to \mathbb{R}$, if $\vec{y}=g(\vec{x})$ and $z=f(\vec{y})$, then:

$$\frac{\partial z}{\partial x_i}=\sum _j\frac{\partial z}{\partial y_j}\frac{\partial y_j}{\partial x_i}$$

In more succinct notation:

$$\nabla {\vec{x}}^z=(\frac{\partial \vec{y}}{\partial \vec{x}}{)}^{\mathsf{T}}\nabla {\vec{y}}^z$$

where the term in the brackets is the Jacobian matrix of $g$.